Question

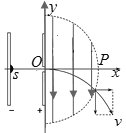
【题目】如图所示，在平面直角坐标系xOy中，y轴左侧有两个正对的极板，极板中心在x轴上，板间电压U0＝1×102V，右侧极板中心有一小孔，左侧极板中心有一个粒子源，能向外释放电荷量q＝1.6×10－8C、质量m＝3.2×10－10kg的粒子（粒子的重力、初速度忽略不计）；y轴右侧以O点为圆心、半径为R＝m的半圆形区域内存在互相垂直的匀强磁场和匀强电场（电场未画出），匀强磁场的的磁感应强度为B＝2T，粒子经电场加速后进入y轴右侧，能沿x轴做匀速直线运动从P点射出。

(1)求匀强电场的电场强度的大小和方向；

(2)若撤去磁场，粒子在场区边缘M点射出电场，求粒子在电场中的运动时间和到M点的坐标；

Answer 1

【答案】(1)200N/m ，y轴负方向；(2)0.01s，（1m，-0.5m）。

【解析】

(1)粒子在板间加速，设粒子到O点时的速度为v0，有

qU0＝m

得：

v0＝＝100m/s

粒子在电磁场中做匀速直线运动，有

qv0B＝qE

可得

E＝v0B＝B＝200N/m

由左手定则判断洛伦兹力沿y轴正方向，所以电场力沿y轴负方向，由于是正电荷，故电场方向沿y轴负方向。

(2)撤去磁场后，粒子进入y轴右侧电场做类平抛运动，轨迹如图所示

对粒子x轴方向有

x1＝v0t1

y轴方向有

y1＝

Eq＝ma

由几何关系可得

联立各式代入数据解得

t1＝0.01s，x1＝1m，y1＝0.5m

所以M点的坐标为（1m，-0.5m）。