题目内容
甲、乙两颗人造卫星绕地球作圆周运动,周期之比为T1:T2=1:8,则它们的轨道半径之 比和运动速率之比分别为( )A.R1:R2=1:4,v1:v2=2:1
B.R1:R2=4:1,v1:v2=2:1
C.R1:R2=1:4,v1:v2=1:2
D.R1:R2=4:1,v1:v2=1:2
【答案】分析:根据人造卫星的万有引力等于向心力,列式求出线速度、角速度、周期和向心力的表达式进行讨论即可.
解答:解:根据万有引力提供向心力
G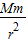 =m
=m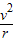 mr(
mr(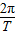 )2,
)2,
r=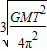 v=
v=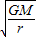
因为TA:TB=1:8
所以RA:RB=1:4
所以VA:VB=2:1
故选A.
点评:本题关键抓住万有引力提供向心力,列式求解出线速度、角速度、周期和向心力的表达式,再进行讨论.
解答:解:根据万有引力提供向心力
G
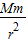 =m
=m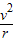 mr(
mr(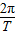 )2,
)2,r=
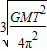 v=
v=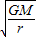
因为TA:TB=1:8
所以RA:RB=1:4
所以VA:VB=2:1
故选A.
点评:本题关键抓住万有引力提供向心力,列式求解出线速度、角速度、周期和向心力的表达式,再进行讨论.

练习册系列答案
相关题目