题目内容
有甲、乙两颗人造卫星绕地球做匀速圆周运动，甲的运行速率比乙大，则下列说法正确的是（ ）
分析：人造卫星绕地球做匀速圆周运动时，由万有引力提供向心力，根据万有引力定律和牛顿第二定律列式，去判断轨道半径、周期、加速度、向心力的关系．
解答：解：根据万有引力提供向心力得：G
=m
=m
r=ma
则得v=
，T=2πr
，a=
，式中M是地球的质量，r是卫星的轨道半径．
所以得知，轨道半径越大，速率越小，周期越大，加速度越小．
由题意，甲的运行速率比乙大，则甲的轨道半径比乙小，甲的运行周期比乙短，甲距离地面的高度一定比乙小，甲的加速度一定比乙大．
由于向心力等于万有引力，由于两个卫星的质量关系未知，不能确定向心力的大小．故ABC错误，D正确．
故选D
| Mm |
| r2 |
| v2 |
| r |
| 4π2 |
| T2 |
则得v=
|
|
| GM |
| r2 |
所以得知，轨道半径越大，速率越小，周期越大，加速度越小．
由题意，甲的运行速率比乙大，则甲的轨道半径比乙小，甲的运行周期比乙短，甲距离地面的高度一定比乙小，甲的加速度一定比乙大．
由于向心力等于万有引力，由于两个卫星的质量关系未知，不能确定向心力的大小．故ABC错误，D正确．
故选D
点评：解决本题的关键掌握万有引力提供向心力这一思路，列式进行分析即可．
练习册系列答案
阅读快车系列答案
相关题目
（1）①假设有两颗人造卫星正环绕月球做匀速圆周运动，甲卫星在近月轨道上运行（忽略离月球表面的高度），周期为T，乙卫星在距离月球表面h高度的轨道上运行，周期为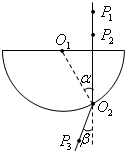
大头针P1、P2的连线与半圆的直径垂直，与圆弧的交点为O2．
