题目内容
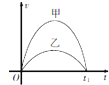
【题目】如图所示,足够长的水平传送带以速度v沿逆时针方向转动,传送带的左端与光滑圆弧轨道底部平滑连接,圆弧轨道上的A点与圆心等高,一小物块从A点静止滑下,再滑上传送带,经过一段时间又返回圆弧轨道,返回圆弧轨道时小物块恰好能到达A点,则下列说法正确的是()

A. 圆弧轨道的半径一定是![]()
B. 若减小传送带速度,则小物块可能到达不了A点
C. 若增加传送带速度,则小物块有可能经过圆弧轨道的最高点
D. 不论传送带速度增加到多大,小物块都不可能经过圆弧轨道的最高点
【答案】BD
【解析】试题分析:当物体在圆轨道上从A点滑到底端时的速度为v0, 根据动能定理可得:mgR=mv02
所以小物块滑上传送带的初速度![]() ,物体到达传送带上之后,受到向左的摩擦力作用开始做匀减速运动,速度减到零之后,又在传送带的摩擦力的作用下向左加速,根据物体的受力可知,物体在减速和加速的过程物体的加速度的大小是相同的,所以物体返回圆轨道时速度大小等于从圆轨道下滑刚到传送带时的速度大小,因此只要传送带的速度
,物体到达传送带上之后,受到向左的摩擦力作用开始做匀减速运动,速度减到零之后,又在传送带的摩擦力的作用下向左加速,根据物体的受力可知,物体在减速和加速的过程物体的加速度的大小是相同的,所以物体返回圆轨道时速度大小等于从圆轨道下滑刚到传送带时的速度大小,因此只要传送带的速度![]() ,物体就能返回到A点.则可知半径满足R≤
,物体就能返回到A点.则可知半径满足R≤![]() 即可,故A错误.当减小传送带速度时,只要传送带的速度满足v≥,物体就能返回到A点.当v≤时,小物块可能到达不了A点,故B正确.若增大传送带的速度,由运动的对称性可知物体还将以下滑时的速度返回圆轨道,所以只能滑到A点,不能滑到圆弧轨道的最高点.故C错误,D正确.所以BD正确。
即可,故A错误.当减小传送带速度时,只要传送带的速度满足v≥,物体就能返回到A点.当v≤时,小物块可能到达不了A点,故B正确.若增大传送带的速度,由运动的对称性可知物体还将以下滑时的速度返回圆轨道,所以只能滑到A点,不能滑到圆弧轨道的最高点.故C错误,D正确.所以BD正确。

【题目】为了探究加速度与力、质量的关系
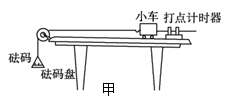
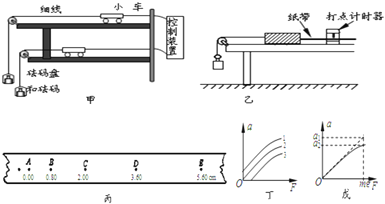
(1)小亮利用如图甲所示的实验方案,探究小车质量一定时加速度与合外力之间的关系,图中上下两层水平轨道,细线跨过滑轮并挂上砝码盘,将砝码和砝码盘的总重作为小车所受合外力,两小车尾部细线连到控制装置上,实验时通过控制装置使两小车同时开始运动,并同时停止.
①实验前,下列操作必要的是
A.选用质量不同的两辆小车 |
B.调节定滑轮的高度,使细线与轨道平行 |
C.使砝码和砝码盘的总质量远小于小车的质量 |
D.将轨道右端适当垫高,使小车在没有细线牵引时能在轨道上匀速运动,以平衡摩擦力 |
②他测量了两小车的位移为x1,x2,则![]() = .
= .
(2)小明用如图乙所示的装置进行实验
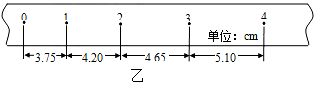
①打出的一条纸带如图丙所示,计时器打点的时间间隔为0.02s.他从比较清晰的A点起,每五个点取一个计数点,测量出各点到A点的距离标在纸带上各点的下方,则小车运动的加速度为 m/s2.(计算结果保留两位有效数字)
②实验前由于疏忽,小明遗漏了平衡摩擦力这一步骤,他测量得到的a﹣F图象,可能是丁图中的图线 (选填“1”、“2”、“3”).
③调整正确后,他作出的a﹣F图象末端明显偏离直线,如果已知小车质量为M,某次所挂钩码质量为m,则戊图中坐标a1应为 ,a2应为 .