��Ŀ����
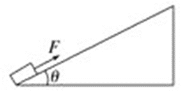
����Ŀ����ͼ��ʾ�����������37�����㹻���Ĺ̶���б�����һ����m��1.0 kg�����壮������б��䶯Ħ����������0.25��������ϸ���������ɾ�ֹ��б�������˶�������F��10 N������ƽ��б�����ϣ���ʱ��t��4.0 s����ͻȻ���ˣ���
��1������ʱ������ٶȴ�С
��2��������������������
��3�������Ӷ��˿�ʼ�������ٷ��ص�б��˵��˶�ʱ��(��֪sin 37����0.60��cos 37����0.80��ȡg��10 m/s2)
���𰸡���1��8.0 m/s ��2��20m����3��4.2 s
��������
�����������������37�����㹻���Ĺ̶���б�����һ����m��1.0 kg����������֪�����⿼��ţ�ٵڶ����ɡ������������˶����ɣ����������������ţ�ٵڶ����ɺ��˶����ɿɽ���⡣
��1���������������ɵã�������б�淽������Ϊ����������Ħ�����������ķ���������ţ�ٵڶ����ɿɵ�
![]()
���
![]()
���ݹ�ʽ�ɵ�
![]()
�������ʱ������ٶ�Ϊ
![]()
��2��������֮���������ȼ����˶����ʼ��ٶ�Ϊ
![]()
���
![]()
���ݹ�ʽ�ɵ�
![]()
��ü��ٽ�λ��Ϊ16m�����ٽ�λ��Ϊ4m�������λ��Ϊ20m��
��3���������˶�ʱ��Ϊt1�������˶�ʱ��Ϊt2,�����˶��ļ��ٶ�Ϊa3�ɹ�ʽ�ɵ�
![]()
���
![]()
��ţ�ٵڶ����ɵ�
![]()
���
![]()
�ɹ�ʽ�ɵ�
![]()
���
![]()
����ʱ��Ϊ
![]()

 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�