题目内容
14．
如图所示，轻细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处，另一端拴一质量为m的小球．当滑块以加速度a=$\sqrt{3}$g向左运动时，g为重力加速度，细线的拉力大小为（ ）| A． | mg | B． | $\sqrt{2}$mg | C． | $\sqrt{3}$mg | D． | 2mg |
分析 求出小球支持力为零时的加速度，判断小球是否离开斜面，再结合牛顿第二定律求出细线的拉力大小．
解答 解：对小球分析，当支持力为零时，根据牛顿第二定律得，F合=mgtan45°=ma，解得a=g$＜\sqrt{3}g$，
可知滑块以加速度a=$\sqrt{3}$g向左运动时，小球离开斜面，根据平行四边形定则知，细线的拉力为：
T=$\sqrt{（ma）^{2}+（mg）^{2}}=2mg$．
故选：D．
点评 本题考查了牛顿第二定律的临界问题，通过牛顿第二定律求出支持力为零时的加速度，判断小球是否离开斜面是关键．
练习册系列答案
阅读快车系列答案
相关题目
4．
如图所示，均匀杆AB重为G，A端用细绳吊在O点，在B端加一水平力F，使AB静止，此时杆与水平方向夹角为α，细绳与竖直方向成θ角，则（ ）
如图所示，均匀杆AB重为G，A端用细绳吊在O点，在B端加一水平力F，使AB静止，此时杆与水平方向夹角为α，细绳与竖直方向成θ角，则（ ）| A． | 拉力F一定大于G | B． | 绳子拉力T一定大于G | ||
| C． | AB杆与水平夹角α必小于θ | D． | F足够大时细绳可在水平方向上 |
物体m在力F作用下沿竖直墙面匀速上升，力F与竖直方向成α角，求动摩擦因数．
3．
一半径为R的雨伞绕柄以角速度ω匀速旋转，如图所示，伞边缘距地面高h，甩出的水滴在地面上形成一个半径为r的圆，则角速度的表达式为（ ）
一半径为R的雨伞绕柄以角速度ω匀速旋转，如图所示，伞边缘距地面高h，甩出的水滴在地面上形成一个半径为r的圆，则角速度的表达式为（ ）| A． | $\frac{r-R}{R}$$\sqrt{\frac{g}{2h}}$ | B． | $\frac{1}{R}$$\sqrt{\frac{g（{r}^{2}-{R}^{2}）}{2h}}$ | C． | $\frac{r}{R}$$\sqrt{\frac{g}{2h}}$ | D． | $\frac{1}{R}$$\sqrt{\frac{g（{r}^{2}+{R}^{2}）}{2h}}$ |
某游戏装置放在竖直平面内，如图所示，装置由粗糙抛物线形轨道AB和光滑的圆弧轨道BCD构成，控制弹射器可将穿在轨道上的小球以不同的水平初速度由A点射入，最后小球将由圆轨道的最高点D水平抛出，落入卡槽中得分，圆弧半径为R，O′为圆弧的圆心，C为圆弧轨道最低点，抛物线轨道上A点在坐标轴的原点O上，轨道与圆弧相切于B点，抛物线轨道方程为y=ax2（0＜a＜$\frac{1}{4R}$），∠BO′C=θ，x轴恰好将半径O′D分成相等的两半，交点为P，x轴与圆弧交于Q点，则：
1．如图甲为远距离输电示意图，变压器均为理想变压器．升压变压器原副线圈匝数比为1：100，其输入电压如图乙所示，远距离输电线的总电阻为100Ω．降压变压器右侧部分为一火警报警系统原理图，其中R1为一定值电阻，R2为用半导体热敏材料制成的传感器，当温度升高时其阻值变小．电压表V显示加在报警器上的电压（报警器未画出）．未出现火警时，升压变压器的输入功率为750kW．下列说法中正确的有（ ）
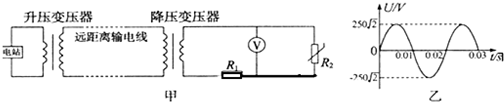
| A． | 降压变压器副线圈输出的交流电频率为100Hz | |
| B． | 远距离输电线路损耗功率为180kw | |
| C． | 当传感器R2所在处出现火警时，输电线上的电流变大 | |
| D． | 当传感器R2所在处出现火警时，电压表V的示数变大 |