题目内容
3. 一半径为R的雨伞绕柄以角速度ω匀速旋转,如图所示,伞边缘距地面高h,甩出的水滴在地面上形成一个半径为r的圆,则角速度的表达式为( )
一半径为R的雨伞绕柄以角速度ω匀速旋转,如图所示,伞边缘距地面高h,甩出的水滴在地面上形成一个半径为r的圆,则角速度的表达式为( )| A. | $\frac{r-R}{R}$$\sqrt{\frac{g}{2h}}$ | B. | $\frac{1}{R}$$\sqrt{\frac{g({r}^{2}-{R}^{2})}{2h}}$ | C. | $\frac{r}{R}$$\sqrt{\frac{g}{2h}}$ | D. | $\frac{1}{R}$$\sqrt{\frac{g({r}^{2}+{R}^{2})}{2h}}$ |
分析 雨滴飞出后做平抛运动,根据高度求出运动的时间,从而求出平抛运动的水平位移,根据几何关系求出水滴在地面上形成圆的半径.
解答 解:根据h=$\frac{1}{2}g{t}^{2}$,解得:t=$\sqrt{\frac{2h}{g}}$,
则平抛运动的水平位移为:s=v${\;}_{0}t=ωR\sqrt{\frac{2h}{g}}$,
根据几何关系得:
r=$\sqrt{{s}^{2}{+R}^{2}}$=R$\sqrt{1+\frac{{2ω}^{2}h}{g}}$
解得:ω=$\frac{1}{R}$$\sqrt{\frac{g({r}^{2}-{R}^{2})}{2h}}$
故选:B.
点评 本题考查了平抛运动和圆周运动的综合,对数学几何能力要求较高,关键作出雨滴在地面上的平面图.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.关于地球同步卫星,下列说法正确的是( )
| A. | 地球同步卫星的轨道平面一定在赤道平面内,但轨道半径可以是任意的 | |
| B. | 地球同步卫星的运动周期大于地球自转的周期 | |
| C. | 地球同步卫星的一定位于地球赤道上空一定高度处,并且相对地面是静止不动的 | |
| D. | 地球对所有同步卫星的万有引力是相等的 |
14. 如图所示,轻细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处,另一端拴一质量为m的小球.当滑块以加速度a=$\sqrt{3}$g向左运动时,g为重力加速度,细线的拉力大小为( )
如图所示,轻细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处,另一端拴一质量为m的小球.当滑块以加速度a=$\sqrt{3}$g向左运动时,g为重力加速度,细线的拉力大小为( )
 如图所示,轻细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处,另一端拴一质量为m的小球.当滑块以加速度a=$\sqrt{3}$g向左运动时,g为重力加速度,细线的拉力大小为( )
如图所示,轻细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处,另一端拴一质量为m的小球.当滑块以加速度a=$\sqrt{3}$g向左运动时,g为重力加速度,细线的拉力大小为( )| A. | mg | B. | $\sqrt{2}$mg | C. | $\sqrt{3}$mg | D. | 2mg |
12.一小球用一轻质弹簧竖直悬挂在升降机中,随升降机一起匀速运动,当突然看到弹簧变短时,升降机的运动情况可能是( )
| A. | 减速下降 | B. | 加速下降 | C. | 减速上升 | D. | 加速上升 |
13.某电容器两端所允许加的最大直流电压是250V.它在正弦交流电路中使用时,交流电压不可以超过是( )
| A. | 250 V | B. | 220 V | C. | 352 V | D. | 177 V |
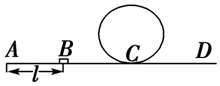 如图是翻滚过山车的模型,光滑的竖直圆规道半径为R=2m,入口的平直轨道AC和出口的平直轨道CD均是粗糙的,质量为m=2kg的小车与水平轨道之间的动摩擦因素均为μ=0.5,加速阶段AB的长度为l=3m,小车从以A静止开始受到水平拉力F=60N的作用,在B点撤去拉力,试问:
如图是翻滚过山车的模型,光滑的竖直圆规道半径为R=2m,入口的平直轨道AC和出口的平直轨道CD均是粗糙的,质量为m=2kg的小车与水平轨道之间的动摩擦因素均为μ=0.5,加速阶段AB的长度为l=3m,小车从以A静止开始受到水平拉力F=60N的作用,在B点撤去拉力,试问: 如图所示,在光滑、固定的水平杆上套着一个光滑的滑环m.滑环下通过一根不可伸长的轻绳悬吊一重物M,轻绳长为L,将滑环固定在水平杆上,给M一个水平冲量作用,使M摆动,且恰好刚碰到水平杆,问:
如图所示,在光滑、固定的水平杆上套着一个光滑的滑环m.滑环下通过一根不可伸长的轻绳悬吊一重物M,轻绳长为L,将滑环固定在水平杆上,给M一个水平冲量作用,使M摆动,且恰好刚碰到水平杆,问: 如图所示,在一二象限-R≤x≤R范围内有竖直向下的匀强电场,场强大小为E,电场的上边界方程为y=$\frac{1}{2R}$x2.在三四象限内存在垂直于纸面向里、边界方程为x2+y2=R2的匀强磁场.现在第二象限中电场的上边界分布有许多质量为m,电量为q的正离子,在y=$\frac{1}{2}$R处有一荧光屏,当正离子达到荧光屏时会发光,不计重力和离子间相互作用力.
如图所示,在一二象限-R≤x≤R范围内有竖直向下的匀强电场,场强大小为E,电场的上边界方程为y=$\frac{1}{2R}$x2.在三四象限内存在垂直于纸面向里、边界方程为x2+y2=R2的匀强磁场.现在第二象限中电场的上边界分布有许多质量为m,电量为q的正离子,在y=$\frac{1}{2}$R处有一荧光屏,当正离子达到荧光屏时会发光,不计重力和离子间相互作用力.