题目内容
如图甲所示,光滑、且足够长的金属轨道处AOB呈抛物线形,满足y=±2
,固定在水平面上,整个轨道电阻不计,在轨导中间(0,0)位置有一个体积较小的阻值为R=2Ω的定值电阻,整个轨道处在一个垂直向下的匀强磁场中,磁感强度为B=0.5T.导轨上放一足够长的金属杆MN,金属杆的电阻不计,现用一拉力F沿水平方向拉金属杆,使金属杆以恒定的速度从左向右滑上轨道.图乙所示为拉力F随x的变化图象,求:

(1)请在杆MN上标出感应电流的方向;
(2)匀速运的速度;
(3)在从0-2.0米范围内,电阻R上产生的焦耳热.
| x |

(1)请在杆MN上标出感应电流的方向;
(2)匀速运的速度;
(3)在从0-2.0米范围内,电阻R上产生的焦耳热.
分析:(1)金属杆向右运动时,金属杆与轨道组成的回路磁通量增加,根据楞次定律判断感应电流的方向;
(2)金属杆匀速运动时,拉力F与安培力二力平衡,由法拉第定律、欧姆定律推导出安培力与速度的关系式,由乙图得到F与x的关系,由平衡条件列式就能求出速度;
(3)根据功能关系可知,拉力所做的功等于电路中产生的焦耳热.由数学知识知,F-x图象的“面积”等于拉力F所做的功.
(2)金属杆匀速运动时,拉力F与安培力二力平衡,由法拉第定律、欧姆定律推导出安培力与速度的关系式,由乙图得到F与x的关系,由平衡条件列式就能求出速度;
(3)根据功能关系可知,拉力所做的功等于电路中产生的焦耳热.由数学知识知,F-x图象的“面积”等于拉力F所做的功.
解答:解:(1)金属杆向右运动时,金属杆与轨道组成的回路磁通量增加,磁场方向向里,根据楞次定律判断得知MN杆上感应电流的方向为N→M;
(2)金属杆的落在轨道上长度为 L=4
产生的感应电动势 E=BLv,
感应电流为 I=
金属杆所受的安培力 FA=BIL=
=
=
=2vx
根据平衡条件得:F=FA=2vx
由(乙)图可知
=
=4
所以v=2m/s
(3)由于金属干做匀速运动,所以外力做的功全部转化成电阻的焦耳热.
在F-x图中,所围的“面积”即为F做的功,在从0-2.0米范围内,
Q=W=
Fx=
×8×2J=8J
答:
(1)在杆MN上标出感应电流的方向为N→M;
(2)匀速运动的速度是2m/s;
(3)在从0-2.0米范围内,电阻R上产生的焦耳热是8J.
(2)金属杆的落在轨道上长度为 L=4
| x |
产生的感应电动势 E=BLv,
感应电流为 I=
| BLv |
| R |
金属杆所受的安培力 FA=BIL=
| B2L2v |
| R |
B2(4
| ||
| R |
| 0.52×16xv |
| 2 |
根据平衡条件得:F=FA=2vx
由(乙)图可知
| F |
| x |
| 12 |
| 3 |
所以v=2m/s
(3)由于金属干做匀速运动,所以外力做的功全部转化成电阻的焦耳热.
在F-x图中,所围的“面积”即为F做的功,在从0-2.0米范围内,
Q=W=
| 1 |
| 2 |
| 1 |
| 2 |
答:
(1)在杆MN上标出感应电流的方向为N→M;
(2)匀速运动的速度是2m/s;
(3)在从0-2.0米范围内,电阻R上产生的焦耳热是8J.
点评:本题既要掌握电磁感应中基本知识,如法拉第定律、楞次定律、安培力公式,同时要运用数学知识求拉力做功.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
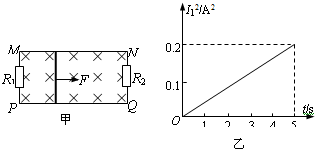 如图甲所示,光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上,两导轨间距为L=1m,定值电阻R1=4Ω,R2=2Ω,导轨上放一质量为m=1kg的金属杆,导轨和金属杆的电阻不计,整个装置处于磁感应强度为B=0.8T的匀强磁场中,磁场的方向垂直导轨平面向下,现用一拉力F沿水平方向拉杆,使金属杆由静止开始运动.图乙所示为通过R1中的电流平方随时间变化的I12-t图线,求:
如图甲所示,光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上,两导轨间距为L=1m,定值电阻R1=4Ω,R2=2Ω,导轨上放一质量为m=1kg的金属杆,导轨和金属杆的电阻不计,整个装置处于磁感应强度为B=0.8T的匀强磁场中,磁场的方向垂直导轨平面向下,现用一拉力F沿水平方向拉杆,使金属杆由静止开始运动.图乙所示为通过R1中的电流平方随时间变化的I12-t图线,求: (2011?崇明县二模)如图甲所示,光滑绝缘的水平面上一矩形金属线圈 abcd的质量为m、电阻为R、面积为S,ad边长度为L,其右侧是有左右边界的匀强磁场,磁场方向垂直纸面向外,磁感应强度大小为B,ab边长度与有界磁场区域宽度相等,在t=0时刻线圈以初速度v0进入磁场,在t=T时刻线圈刚好全部进入磁场且速度为vl,此时对线圈施加一沿运动方向的变力F,使线圈在t=2T时刻线圈全部离开该磁场区,若上述过程中线圈的v-t图象如图乙所示,整个图象关于t=T轴对称.则下列各项正确的是( )
(2011?崇明县二模)如图甲所示,光滑绝缘的水平面上一矩形金属线圈 abcd的质量为m、电阻为R、面积为S,ad边长度为L,其右侧是有左右边界的匀强磁场,磁场方向垂直纸面向外,磁感应强度大小为B,ab边长度与有界磁场区域宽度相等,在t=0时刻线圈以初速度v0进入磁场,在t=T时刻线圈刚好全部进入磁场且速度为vl,此时对线圈施加一沿运动方向的变力F,使线圈在t=2T时刻线圈全部离开该磁场区,若上述过程中线圈的v-t图象如图乙所示,整个图象关于t=T轴对称.则下列各项正确的是( )
 ,固定在水平面上,整个轨道电阻不计,在轨导中间(0,0)位置有一个体积较小的阻值为R=2Ω的定值电阻,整个轨道处在一个垂直向下的匀强磁场中,磁感强度为B=0.5T. 导轨上放一足够长的金属杆MN,金属杆的电阻不计,现用一拉力F沿水平方向拉金属杆,使金属杆以恒定的速度从左向右滑上轨道. 图乙所示为拉力F随x的变化图像,求:
,固定在水平面上,整个轨道电阻不计,在轨导中间(0,0)位置有一个体积较小的阻值为R=2Ω的定值电阻,整个轨道处在一个垂直向下的匀强磁场中,磁感强度为B=0.5T. 导轨上放一足够长的金属杆MN,金属杆的电阻不计,现用一拉力F沿水平方向拉金属杆,使金属杆以恒定的速度从左向右滑上轨道. 图乙所示为拉力F随x的变化图像,求: