题目内容
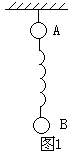
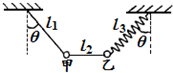
如图所示,质量均为m的甲、乙两个小球用长度分别为l1、l2的两根不可伸长的轻质细线及长度为l3的轻弹簧连接起来,l1、l3的一端悬挂在天花板上,与竖直方向夹角都为θ,l2水平拉直,两个球处于静止状态.现将细线l2从中间剪断,则剪断瞬间甲、乙两小球的加速度分别为( )
| A.gsinθ,gtanθ | B.gcosθ,gsinθ |
| C.gtanθ,gsinθ | D.gtanθ,gcosθ |

将细线l2从中间剪断后,甲球做圆周运动,剪断细线的瞬间,加速度方向沿轨迹的切线方向,由牛顿第二定律得:
mgsinθ=ma甲,
解得:a甲=gsinθ;
弹簧的弹力不可突变,将细线l2从中间剪断瞬间,对乙球,由牛顿第二定律得:
mgtanθ=ma乙,
解得:a乙=gtanθ;
故选:A.
mgsinθ=ma甲,
解得:a甲=gsinθ;
弹簧的弹力不可突变,将细线l2从中间剪断瞬间,对乙球,由牛顿第二定律得:
mgtanθ=ma乙,
解得:a乙=gtanθ;
故选:A.

练习册系列答案
相关题目