题目内容
【题目】如图所示，边长为4l的正方形ABCD内存在两个场强大小相等、方向相反的有界匀强电场，中位线OO/上方的电场方向竖直向下，OO/下方的电场方向竖直向上。从某时刻起，在A、O两点间（含A点，不含O点）连续不断地有电量为+q、质量为m的粒子以相同速度v0沿水平方向射入电场。其中从A点射入的粒子第一次穿越OO/后就恰好从C点沿水平方向射出正方形电场区。不计粒子的重力及粒子间的相互作用。求：
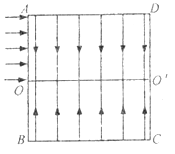
（1）从AO间入射的粒子穿越电场区域的时间t和匀强电场的场强E的大小；
（2）在AO间离O点高度h为多大的粒子，最终能沿水平方向从CD间射出正方形电场区？
（3）上一问中能沿水平方向射出正方形电场区的这些粒子，在穿越OO/时的速度大小v
【答案】（1）
（2）
(n=1,2,3…)（3）v0
(n=1,2,3……)
【解析】试题分析：粒子在电场中做类平抛运动，由类平抛运动可以求出粒子的运动时间与电场强度；作出粒子运动轨迹，粒子在电场中做类平抛运动，由类平抛运动规律可以求出高度h；由动能定理可以求出粒子的速度。
（1）带电粒子先类平抛后类斜抛，运动轨迹如图1所示：
在水平方向上，做匀速直线运动所以运动时间为： 
又因为竖直方向先匀加速运动： 
联立以上可得： 
(2) 满足题意的带电粒子运动轨迹如图2所示，每小段抛物线的水平长度为
，则：
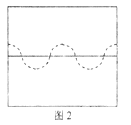
， 其中： 
结合（1）中的E解得： 
（3）由题意粒子每次到达中位线的速度大小相同，从进入电场到第一次到达中位线过程，
由动能定理得： 
解得： 
练习册系列答案
相关题目
