题目内容
6. 如图所示,一斜面倾角为θ=30°,小球以初动能3J水平抛出,不计空气阻力,若小球落在斜面上位移最小,则小球落在斜面上的动能为( )
如图所示,一斜面倾角为θ=30°,小球以初动能3J水平抛出,不计空气阻力,若小球落在斜面上位移最小,则小球落在斜面上的动能为( )| A. | 4J | B. | 7J | C. | 36J | D. | 39J |
分析 当小球落在斜面上位移最小,即位移的方向与斜面垂直,根据速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,求出速度方向与水平方向的夹角正切值,从而求出竖直分速度,结合平行四边形定则求出速度,从而求出小球落在斜面上的动能.
解答 解:小球落在斜面上的位移最小,知位移的方向与斜面垂直,即位移与水平方向的夹角为60°,
则速度方向与水平方向的夹角的正切值$tanα=2tan60°=2\sqrt{3}$,
因为$tanα=\frac{{v}_{y}}{{v}_{0}}$,解得${v}_{y}=2\sqrt{3}{v}_{0}$,
则落在斜面上的速度$v=\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=\sqrt{13}{v}_{0}$,
因为$\frac{1}{2}m{{v}_{0}}^{2}=3J$,则落在斜面上的动能${E}_{k}=\frac{1}{2}m{v}^{2}=13×3J=39J$.
故选:D.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍进行求解.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
1.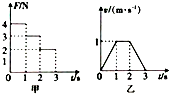 一滑块静止在水平面上,t=0时刻在滑块上施加一水平力F,力F和滑块的速度v随时间的变化规律分别如图甲、乙所示,g取10m/s2,则下列说法正确的是( )
一滑块静止在水平面上,t=0时刻在滑块上施加一水平力F,力F和滑块的速度v随时间的变化规律分别如图甲、乙所示,g取10m/s2,则下列说法正确的是( )
 一滑块静止在水平面上,t=0时刻在滑块上施加一水平力F,力F和滑块的速度v随时间的变化规律分别如图甲、乙所示,g取10m/s2,则下列说法正确的是( )
一滑块静止在水平面上,t=0时刻在滑块上施加一水平力F,力F和滑块的速度v随时间的变化规律分别如图甲、乙所示,g取10m/s2,则下列说法正确的是( )| A. | 力F在第1s内做的功为2J | B. | 力F在第1s内做的功为4J | ||
| C. | 滑块与水平面间的摩擦力大小为2N | D. | 力F在第2s内做的功的功率为3W |
18.关于匀速运动,下列说法中正确的是( )
| A. | 匀速运动的质点的运动轨迹是曲线 | |
| B. | 质点运动的速度大小不变,则质点的运动就是匀速运动 | |
| C. | 在相等的时间内通过的路程相等,则此运动一定是匀速直线运动 | |
| D. | 匀速运动是质点的运动速度大小与方向都不变的运动 |


 相距为L的点电荷A、B带电荷量分别为+9Q和-Q,如图所示,今引入第三个点电荷C,使三个点电荷都处于平衡状态,则第三个电荷C应带何种电荷、应放置何处、电荷量是多少?
相距为L的点电荷A、B带电荷量分别为+9Q和-Q,如图所示,今引入第三个点电荷C,使三个点电荷都处于平衡状态,则第三个电荷C应带何种电荷、应放置何处、电荷量是多少? 如图所示,R3=0.2Ω,S断开时,两表读数分别0.4A和2.4V,S闭合时,它们的读数分别变化了0.3A和0.3V.求:
如图所示,R3=0.2Ω,S断开时,两表读数分别0.4A和2.4V,S闭合时,它们的读数分别变化了0.3A和0.3V.求: 如图所示,甲、乙两车沿着同一条平直公路同向行驶,甲车以速度20m/s做匀速运动,乙车原来速度为4m/s,从距甲车114m处以大小为lm/s2的加速度做匀加速运动.(取$\sqrt{1936}=44$)求:
如图所示,甲、乙两车沿着同一条平直公路同向行驶,甲车以速度20m/s做匀速运动,乙车原来速度为4m/s,从距甲车114m处以大小为lm/s2的加速度做匀加速运动.(取$\sqrt{1936}=44$)求: