Question

MN是竖直放置的长L=0.5m的平面镜，观察者在A处观察，有一小球在某处自由下落，小球下落的轨迹与平面
镜相距d=0.25m，观察者能在镜中看到小球像的时间△t=0.2s，已知观察者的眼睛到镜面的距离s=0.5m，求小球从静止开始下落经多长时间，观察者才能在镜中看到小球的像．（要求正确作出光路图，g=10m/s²）

Answer 1

分析：当小球发出的光线经过平面镜反射射入观察者的眼睛时，人就能看到小球镜中的像．根据反射定律作出光路图及边界光线．运用三角形相似法求出人能看到的小球运动区域，再根据小球自由落体运动的规律求时间．

解答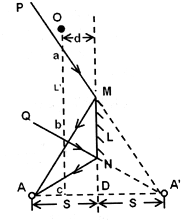：解：正确作出光路图如图．
由平面镜成像规律及光路可逆可知，人在A处，能够观察到平面镜中虚像所对应的空间区域在如图所示的直线PM和QN所包围的区域中，小球在这一区间里运动的距离为图中ab的长度L′．
由于△aA′b∽△MA′N，△bA′c∽△NA′D，有
 

L′

L

=

bA′

NA′

  

bA′

NA′

=

s+d

s

联立求解：L′=0.75m
设小球从静止下落时t人能看到，则：
L′=

1

2

g（t+△t）²-

1

2

gt2
代人数据得 t=0.274s
答：小球从静止开始下落经0.275s观察者才能在镜中看到小球的像．

点评：本题是边界问题，根据反射定律作出边界光线，再根据几何知识和运动学公式结合求解．