Question

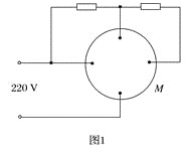
【题目】利用悬停直升机空投救灾物资(如图甲)时对于有些物资只能从不高于h=20m处自由释放才能安全着地，但实际直升机能够安全悬停的高度比h要高得多，直接空投会造成损失。为解决这一问题，研究小组设计了一台限速装置，不论从多高处释放物资，最终都能以安全速度着地。该装置简化工作原理如图乙所示，竖直绝缘圆盘可以绕圆心O自由转动，其上固定半径分别为r1=1m和r2=0.5m的两个同心金属圆环，连接两圆环的金属杆EF的延长线通过圆心O，足够长的不可伸长的轻质细绳一端缠绕在大金属圆环上，另一端通过光滑滑轮挂救灾物资，圆环上的a点和b点通过电刷连接可调电阻R，两圆环之间区域存在垂直于圆盘平面向内的勺强磁场，磁感应强度B=40T。(细绳与大金属圆环间没有滑动，金属杆、金属圆环、导线及电刷的电阻均不计，空气阻力及一切摩擦均不计，重力加速度g=10m/s+)

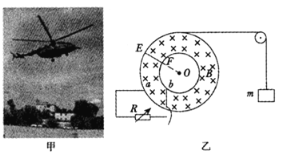
(1)求医药物资能安全着地的最大速度；

(2)利用该装置使医药物资以最大安全速度匀速下降，求此时电阻R两端的电势差；

(3)若医药物资的质量m=60kg，应如何设置可调电阻R的阻值?

(4)试推导质量为m的医药物资在匀速下降时，金属杆EF所受安培力与重力的大小关系。

Answer 1

【答案】（1）20m/s （2）300V （3）R7.5Ω （4）F=mg

【解析】

根据自由落体运动位移与速度公式，即可求解；根据法拉第电磁感应定律，结合几何关系求得面积，从而求得电阻R两端的电势差；由能量守恒关系，重力的功率等于发热功率，从而求得可调电阻的阻值范围；根据安培力表达式F=BIL，结合，和，即可求解；

(1)设医药物资安全到达地面的最大速度为v，

根据自由落体运动可知，则有：

解得：

(2)在t时间内，金属杆EF扫过的面积为：

由法拉第电磁感应定律，金属杆上感应电动势的大小为：

解得：

则电阻R两端的电势差为300V

(3)医药物资以最大安全速度下降时，由功率相等可知：

解得：

可调电阻R的阻值应小于7.5Ω

(4)设金属杆EF所受安培力为F，则有：

将和代入，解得：