题目内容
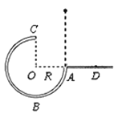
【题目】一个内壁光滑的3/4圆管轨道ABC竖直放置,轨道半径为R。O、A、D位于同一水平线上,A、D间的距离为R.质量为m的小球(球的直径略小于圆管直径),从管口A正上方由静止释放,要使小球能通过C点落到AD区,则球经过C点时( )
A. 对管的作用力大小满足![]()
B. 对管的作用力大小满足![]()
C. 速度大小满足![]()
D. 速度大小满足![]()
【答案】C
【解析】
小球离开C点后做平抛运动,由平抛运动的规律求解C点的速度大小范围.由于球的直径略小于圆管直径,所以管对球的作用力可能向上也可能向下,根据牛顿第二定律分析这两种情况下球对管的作用力大小范围.
小球离开C点做平抛运动,落到A点时水平位移为R,竖直下落高度为R,根据运动学公式可得:竖直方向有:R=![]() gt2;水平方向有:R=vC1t;解得:vC1=
gt2;水平方向有:R=vC1t;解得:vC1=![]() ;小球落到D点时水平位移为2R,则有 2R=vC2t;解得 vC2=
;小球落到D点时水平位移为2R,则有 2R=vC2t;解得 vC2=![]() ;故速度大小满足
;故速度大小满足![]() ≤vc≤
≤vc≤![]() ,故C正确,D错误。由于球的直径略小于圆管直径,所以过C点时,管壁对小球的作用力可能向下,也可能向上,当vC1=
,故C正确,D错误。由于球的直径略小于圆管直径,所以过C点时,管壁对小球的作用力可能向下,也可能向上,当vC1=![]() ,向心力F=
,向心力F=![]() <mg,所以管壁对小球的作用力向上,根据牛顿第二定律得:mg-Fc1=
<mg,所以管壁对小球的作用力向上,根据牛顿第二定律得:mg-Fc1=![]() ,解得N=
,解得N=![]() mg;当vC′=
mg;当vC′=![]() ,向心力F′=
,向心力F′=![]() =2mg>mg,所以管壁对小球的作用力向下,根据牛顿第二定律得:mg+Fc2=
=2mg>mg,所以管壁对小球的作用力向下,根据牛顿第二定律得:mg+Fc2=![]() ,解得N′=mg;假设在C点管壁对小球的作用力为0时的速度大小为vC3,则由向心力公式可得
,解得N′=mg;假设在C点管壁对小球的作用力为0时的速度大小为vC3,则由向心力公式可得![]() ,解得vC3=
,解得vC3=![]() ,vC3在
,vC3在![]() ≤vc≤
≤vc≤![]() 范围内,所以满足条件。所以球经过C点时对管的作用力大小满足0≤Fc≤mg,故AB错误。故选C。
范围内,所以满足条件。所以球经过C点时对管的作用力大小满足0≤Fc≤mg,故AB错误。故选C。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目