题目内容
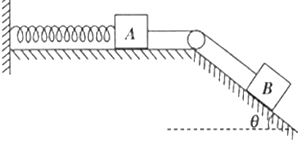
【题目】质量m=1.0kg的物块A(可视为支点)轻弹簧的上端连接,弹簧下端固定在光滑斜面底端,斜面的倾斜角![]() =30°。平衡时,弹簧的压缩量为x=0.20m,此时具有的弹性势能Ep=0.50J,物块A处在O时弹簧为原长,如图所示。一质量m=1.0kg物块B(可视为质点)从距离物块A为d=2.0m处从静止开始沿斜面下滑,与物体A发生碰撞后立刻一起向下运动,但不粘连,它们到达最低点后又向上运动。,g=10m/s2,求:
=30°。平衡时,弹簧的压缩量为x=0.20m,此时具有的弹性势能Ep=0.50J,物块A处在O时弹簧为原长,如图所示。一质量m=1.0kg物块B(可视为质点)从距离物块A为d=2.0m处从静止开始沿斜面下滑,与物体A发生碰撞后立刻一起向下运动,但不粘连,它们到达最低点后又向上运动。,g=10m/s2,求:
(1)物块B与物体A碰撞后的速度;
(2)物块B向上运动到达的最高点与O的距离s。

【答案】(1)v共=![]() m/s;(2)S=
m/s;(2)S=![]() =0.35m
=0.35m
【解析】
(1)B物体的加速度:a=gsin![]() =5m/s2
=5m/s2
有匀变速直线运动的速度位移公式:v2=2ad
得![]()
AB碰撞过程中系统动量守恒,以沿斜面向下为正方向,
根据动量守恒定律得:mv=2mv共,
解得:v共=![]() m/s
m/s
(2)碰后AB和弹簧组成的系统机械能守恒,并且AB在弹簧处分离,设AB分离瞬间速度为v′,根据机械能守恒定律得:
![]()
解得:![]() m/s
m/s
此后,B向上做匀减速运动,上升距离为:S=![]() =0.35m
=0.35m

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目