题目内容
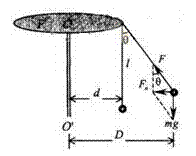
某游乐场中有一种叫“空中飞椅”的游乐设施，其基本装置是将绳子上端固定在转盘上，绳子下端连接座椅，人坐在飞椅上随转盘旋转而在空中飞旋。若将人看成质点，则可简化为如图所示的物理模型。其中P为处于水平面内的转盘，可绕竖直转轴OO′转动，设轻绳长L=10m，人的质量m=60kg，转盘静止时人与转轴之间的距离d=4m.转盘慢慢加速运动，经过一段时间后转速保持稳定，此时人与转轴之间的距离变为D=10m且保持不变。不计空气阻力，绳子不可伸长，取g=10m/s2。求：
（1）最后转盘匀速转动时的角速度大约为多少？
（2）转盘从静止到启动后达到稳定状态这一过程中，绳子对人做了多少功？
（3）若转盘稳定转动后，一位游客随身带的手机突然滑下来，此时座椅离地面H=5米，在地面上的管理员发现这一情况后，跑过来接，如果管理员在转轴中心处，问他至少应该跑多远才行？
解析： （1）设转盘匀速转动时绳子与竖直方向间的夹角为θ，质点所处的位置和受力情况如图所示，可得
①（1分）
人所受合力提供向心力
Fn=mgtanθ=mω2D ②（2分）
代入数据解得ω=0.866rad/s ③（1分）
（2）质点上升的高度
h=L（1－cosθ）=2m ④（1分）
人匀速转动时的线速度
v=ωD ⑤（1分）
转盘从静止启动到转速稳定这一过程，绳子对人做的功等于人机械能的增加量
W=
mv2+mgh ⑥（1分）
代入数据解得W=3450 J ⑦ （2分）
（3）手机滑下来后沿圆周的切线方向平抛运动，设手机从抛出至落地的水平距离为x，则 x=vt（1分）
手机下落时间为t，有H=gt2（1分）
管理员跑动的距离为
（1分）
联立解得s=13.2m. （2分）
某游乐场中有一种叫“空中飞椅”的游乐设施，其基本装置是将绳子上端固定在转盘的边缘上，绳子下端连接座椅，人坐在座椅上随转盘旋转而在空中飞旋．若将人和座椅看成是一个质点，则可简化为如图所示的物理模型．其中P为处于水平面内的转盘，可绕竖直转轴OO′转动，设绳长l=10m，质点的质量m=60kg，转盘静止时质点与转轴之间的距离dd=4m．转盘逐渐加速转动，经过一段时间后质点与转盘一起做匀速圆周运动，此时绳与竖直方向的夹角θ=37°．（不计空气阻力及绳重，绳子不可伸长，sin37°=0.6，cos37°=0.8，g=10m/s2）求：
某游乐场中有一种叫“空中飞椅”的游乐设施，其基本装置是将绳子上端固定在转盘的边缘上，绳子下端连接座椅，人坐在座椅上随转盘旋转而在空中飞旋．若将人和座椅看成是一个质点，则可简化为如图所示的物理模型．其中P为处于水平面内的转盘，可绕竖直转轴OO′转动，设绳长l=10m，质点的质量m=60kg，转盘静止时质点与转轴之间的距离d=4m．转盘逐渐转动起来，经过一段时间后质点与转盘一起做匀速圆周运动，此时绳与竖直方向的夹角θ=37°．（不计空气阻力及绳重，绳子不可伸长，sin37°=0.6，cos37°=0.8，g=10m/s2）求：质点与转盘一起做匀速圆周运动时转盘的角速度及绳子的拉力．
某游乐场中有一种叫“空中飞椅”的游乐设施，其基本装置是将绳子上端固定在转盘的边缘上，绳子下端连接座椅，人坐在座椅上随转盘旋转而在空中飞旋．若将人和座椅看成是一个质点，则可简化为如图的物理模型．其中P为处于水平面内的转盘，可绕竖直转轴OO′转动，设绳长l=10m，质点的质量m=60kg，转盘静止时质点与转轴之间的距离d=4m．转盘逐渐加速转动，经过一段时间后质点与转盘一起做匀速圆周运动，此时绳与竖直方向的夹角θ=370．（不计空气阻力及绳重，绳子不可伸长，sin37°=0.6，cos37°=0.8，g=10m/s2）求：
某游乐场中有一种叫“空中飞椅”的游乐设施，其基本装置是将绳子上端固定在转盘上，绳子下端连接座椅，人坐在飞椅上随转盘旋转而在空中飞旋．若将人与座椅看成质点，则可简化为如图所示的物理模型．其中P为处于水平面内的转盘，可绕竖直转轴OO′转动，设轻绳长L=10m，人与座椅的总质量m=60kg，转盘静止时人与转轴之间的距离d=4m，此时座椅离地面H=3m．转盘慢慢加速运动，经过一段时间后转速保持稳定，此时人与转轴之间的距离变为D=10m且保持不变．不计空气阻力，绳子不可伸长，取g=10m/s2．问：