题目内容
18.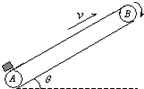 图示为一倾角θ=30°的传送带装置示意图,绷紧的传送带在A、B间始终保持v=1m/s的恒定速率向上运行,一个质量m=2kg的物体无初速地放在A处,传送带就将物体传送上去.设物体与传送带间的滑动摩擦力f=0.6mg,AB间的距离L=4m,g取10m/s2.求物体从A处传送到B处所需的时间t.
图示为一倾角θ=30°的传送带装置示意图,绷紧的传送带在A、B间始终保持v=1m/s的恒定速率向上运行,一个质量m=2kg的物体无初速地放在A处,传送带就将物体传送上去.设物体与传送带间的滑动摩擦力f=0.6mg,AB间的距离L=4m,g取10m/s2.求物体从A处传送到B处所需的时间t.
分析 物块放上传送带先做匀加速直线运动,当物块达到传送带速度时,和传送带一起做匀速直线运动.结合牛顿第二定律和运动学公式求出物体从A处传送到B处所需的时间.
解答 解:物体开始时做匀加速运动,由牛顿定律得加速度为:
$a=\frac{f-mgsinθ}{m}=\frac{0.6mg-0.5mg}{m}=1m/{s}^{2}$
物体从静止运动到速度等于v经过得时间为t1,则有:
${t}_{1}=\frac{v}{a}=\frac{1}{1}=1s$
t1时间内物体的位移为:
$s=\frac{1}{2}a{t}^{2}=0.5m$
因为s<L,物体此后做匀速向上运动,匀速运动时间为:
${t}_{2}=\frac{L-s}{v}=\frac{4-0.5}{1}=3.5s$
因此,物体从A处传送到B处所需的时间为:t=t1+t2=4.5s
答:物体从A处传送到B处所需的时间t为4.5s.
点评 解决本题的关键理清物块的运动情况,结合牛顿第二定律和运动学公式进行求解.注意物体运动的过程分析和受力分析的准确性.

练习册系列答案
相关题目
9.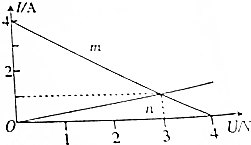 如图所示的电源的电流与路端电压的关系曲线中,m、n分别为电源和定值电阻的图线,则以下说法正确的是( )
如图所示的电源的电流与路端电压的关系曲线中,m、n分别为电源和定值电阻的图线,则以下说法正确的是( )
 如图所示的电源的电流与路端电压的关系曲线中,m、n分别为电源和定值电阻的图线,则以下说法正确的是( )
如图所示的电源的电流与路端电压的关系曲线中,m、n分别为电源和定值电阻的图线,则以下说法正确的是( )| A. | 该电源的内阻r=0.5Ω | |
| B. | 定值电阻的阻值为$\frac{1}{3}$Ω | |
| C. | 如果将电阻直接接在该电源上,则该定值电阻消耗的电功率为4W | |
| D. | 改变负载,电源的最大输出功率为为4W |
6. 三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°.现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,(g取10m/s2,sin37°=0.6,cos37°=0.8)下列说法正确的是( )
三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°.现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,(g取10m/s2,sin37°=0.6,cos37°=0.8)下列说法正确的是( )
 三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°.现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,(g取10m/s2,sin37°=0.6,cos37°=0.8)下列说法正确的是( )
三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°.现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,(g取10m/s2,sin37°=0.6,cos37°=0.8)下列说法正确的是( )| A. | 物块A先到达传送带底端 | |
| B. | 物块A、B同时到达传送带底端 | |
| C. | 物块A、B到达传送带底端时速度大小相等 | |
| D. | 物块A、B在传送带上的划痕长度之比为1:3 |
10.某时刻,一列横波的图象如图所示,由图可知( )
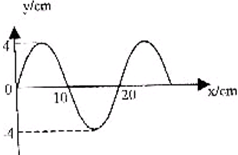

| A. | 波长为20cm,振幅为4cm | B. | 波长为10cm,振幅为4cm | ||
| C. | 波长为10cm,振幅为8cm | D. | 波长为20cm,振幅为8cm |
7.关于物体的重心,下列说法正确的是( )
| A. | 物体的重心一定在物体上 | |
| B. | 物体重心的位置与质量分布和几何形状有关 | |
| C. | 任何物体的重心都在几何中心 | |
| D. | 物体的形状发生改变,其重心的位置一定改变 |

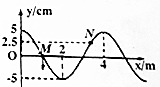 如图为一列简谐横波在t1=0时刻的波形图,此时质点M正处于平衡位置且沿y轴负方向运动,到t2=0.7s时质点M恰好第二次到达y轴正方向的最大位移处,求:
如图为一列简谐横波在t1=0时刻的波形图,此时质点M正处于平衡位置且沿y轴负方向运动,到t2=0.7s时质点M恰好第二次到达y轴正方向的最大位移处,求: 某种型号的汽车,装有储能装置,能够将减速时的部分动能转化并储存在蓄电池中,为蓄电池充电.让这种型号的汽车以额定功率行驶一段距离后关闭发动机,重复这个过程并进行反复测试,得到了汽车动能E与位移x的关系如图所示,其中a是始终关闭储能装置的关系图线,b是关闭发动机后即开启储能装置的关系图线.已知汽车的质量为1.25×103kg,设汽车运动过程中所受地面阻力恒定,空气阻力不计.该储能装置将其他形式的能转化成电能的效率是25%.求:
某种型号的汽车,装有储能装置,能够将减速时的部分动能转化并储存在蓄电池中,为蓄电池充电.让这种型号的汽车以额定功率行驶一段距离后关闭发动机,重复这个过程并进行反复测试,得到了汽车动能E与位移x的关系如图所示,其中a是始终关闭储能装置的关系图线,b是关闭发动机后即开启储能装置的关系图线.已知汽车的质量为1.25×103kg,设汽车运动过程中所受地面阻力恒定,空气阻力不计.该储能装置将其他形式的能转化成电能的效率是25%.求: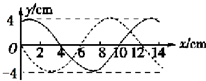 如图所示,实线是一列沿x轴传播的简谐横波在t=0时刻的波的图象,虚线为这列波在t=0.05s时刻的波的图象.已知该波的波速为80cm/s,则下列说法正确的BCD.
如图所示,实线是一列沿x轴传播的简谐横波在t=0时刻的波的图象,虚线为这列波在t=0.05s时刻的波的图象.已知该波的波速为80cm/s,则下列说法正确的BCD.