题目内容
13. 如图为一列简谐横波在t1=0时刻的波形图,此时质点M正处于平衡位置且沿y轴负方向运动,到t2=0.7s时质点M恰好第二次到达y轴正方向的最大位移处,求:
如图为一列简谐横波在t1=0时刻的波形图,此时质点M正处于平衡位置且沿y轴负方向运动,到t2=0.7s时质点M恰好第二次到达y轴正方向的最大位移处,求:(1)该列波的传播方向和波速大小;
(2)从t1=0到t3=1.0s时间内质点N通过的路程;
(3)质点N在t3=1.0s时偏离平衡位置的位移.
分析 (1)质点P点沿y轴负方向,运用波形的平移法可判断出波的传播方向.
由波动图象读出波长.根据条件:当t=0.7s时质点P恰好第2次到达y轴正方向最大位移处,则有1$\frac{3}{4}$T=t,即可求出周期,由波速公式v=$\frac{λ}{T}$求出波速.
(2)质点在一个周期内通过的路程是四个振幅,根据从t1=0到t3=1.0s的时间与周期的关系,求出质点N运动的路程S.
(3)根据在t3=1.0s时与周期的关系,确定质点N的位置,即可求得相对于平衡位置的位移y的大小.
解答 解:(1)质点P点沿y轴负方向,由波形的平移法判断可知此波沿x轴负向传播.
在t1=0到t2=0.7 s这段时间里,质点P恰好第2次到达y正方向最大位移处
则有(1+$\frac{3}{4}$)T=0.7 s
解得T=0.4 s
由图象可得简谐波的波长为λ=0.4m
则波速v=$\frac{λ}{T}$=$\frac{0.4}{0.4}$=1 m/s
(2)在t1=0至t3=1.0 s这段时间,质点N恰经过了2$\frac{1}{2}$个周期,
由于振幅A=5 cm,所以质点N运动的路程为S=4A×2+2A=10×5cm=50cm
(3)质点N经过2$\frac{1}{2}$个周期后恰好到关于x轴与N点对称的位置,则相对于平衡位置的位移为y=-2.5cm
答:
(1)该简谐横波的波速v的大小为1m/s,方向沿x轴负向;
(2)从t1=0到t3=1.0s时间内质点N通过的路程50cm;
(3)质点N在t3=1.0s时偏离平衡位置的位移-2.5cm.
点评 本题关键要理解波的周期性,求出波的周期,考查把握质点的振动与波动之间联系的能力,质点不会随波迁移的,同时注意位移有大小,且有方向.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
3.王飞同学在用一根弹簧制作弹簧测力计的实验时,在弹簧的下端挂不同重力的钩码,对应的弹簧的长度也不同.具体数据见下表.请你分析表中这些实验数裾.你得到的一个重要的实验结论是:
弹簧的伸长量与弹力成正比;弹簧的原长为23cm.
弹簧的伸长量与弹力成正比;弹簧的原长为23cm.
| 钩码重力G/N | 1 | 2 | 3 | 4 | 5 |
| 弹簧长度/cm | 25 | 27 | 29 | 31 | 33 |
1. 图甲为一列简谐波在某一时刻的波形图,Q、P是波上的质点,图乙为质点P以此时刻为计时起点的振动图象,下列说法中正确的是 ( )
图甲为一列简谐波在某一时刻的波形图,Q、P是波上的质点,图乙为质点P以此时刻为计时起点的振动图象,下列说法中正确的是 ( )
 图甲为一列简谐波在某一时刻的波形图,Q、P是波上的质点,图乙为质点P以此时刻为计时起点的振动图象,下列说法中正确的是 ( )
图甲为一列简谐波在某一时刻的波形图,Q、P是波上的质点,图乙为质点P以此时刻为计时起点的振动图象,下列说法中正确的是 ( )| A. | 经过O.05s时,质点Q的加速度大于质点P的加速度 | |
| B. | 经过O.05s时,质点Q的加速度小于质点P的加速度 | |
| C. | 经过O.1s时,质点Q的运动方向沿y轴负方向 | |
| D. | 此列波沿x轴正方向传播,波速为20m/s | |
| E. | 经过O.1s时,质点Q的运动方向沿y轴正方向. |
5.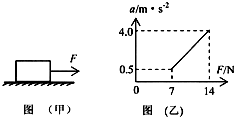 如图(甲)所示,物体原来静止在水平面上,今用一水平外力F拉物体,在外力F从0开始逐渐增大的过程中,物体先静止后做变加速运动,其加速度a随外力F变化的图象如图(乙)所示.根据图(乙)中所标示数据可计算出( )
如图(甲)所示,物体原来静止在水平面上,今用一水平外力F拉物体,在外力F从0开始逐渐增大的过程中,物体先静止后做变加速运动,其加速度a随外力F变化的图象如图(乙)所示.根据图(乙)中所标示数据可计算出( )
 如图(甲)所示,物体原来静止在水平面上,今用一水平外力F拉物体,在外力F从0开始逐渐增大的过程中,物体先静止后做变加速运动,其加速度a随外力F变化的图象如图(乙)所示.根据图(乙)中所标示数据可计算出( )
如图(甲)所示,物体原来静止在水平面上,今用一水平外力F拉物体,在外力F从0开始逐渐增大的过程中,物体先静止后做变加速运动,其加速度a随外力F变化的图象如图(乙)所示.根据图(乙)中所标示数据可计算出( )| A. | 物体的质量 | B. | 物体与水平面之间的滑动摩擦力 | ||
| C. | 物体与水平之间的最大静摩擦力 | D. | 在外力F为14N时,物体的速度最大 |
2.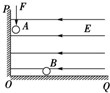 如图所示,两个相互垂直的光滑绝缘固定挡板PO、OQ竖直放置在匀强电场E中,场强方向水平向左且垂直于挡板PO,图中A、B两球(可视为质点)质量相同且均带正电荷.当A球受竖直向下推力F作用时,A、B两球均紧靠挡板处于静止状态,这时两球之间的距离L;若使球A在推力F作用下沿挡板PO向O点移动一小段距离后,球A与球B重新处于静止状态,在此过程中( )
如图所示,两个相互垂直的光滑绝缘固定挡板PO、OQ竖直放置在匀强电场E中,场强方向水平向左且垂直于挡板PO,图中A、B两球(可视为质点)质量相同且均带正电荷.当A球受竖直向下推力F作用时,A、B两球均紧靠挡板处于静止状态,这时两球之间的距离L;若使球A在推力F作用下沿挡板PO向O点移动一小段距离后,球A与球B重新处于静止状态,在此过程中( )
 如图所示,两个相互垂直的光滑绝缘固定挡板PO、OQ竖直放置在匀强电场E中,场强方向水平向左且垂直于挡板PO,图中A、B两球(可视为质点)质量相同且均带正电荷.当A球受竖直向下推力F作用时,A、B两球均紧靠挡板处于静止状态,这时两球之间的距离L;若使球A在推力F作用下沿挡板PO向O点移动一小段距离后,球A与球B重新处于静止状态,在此过程中( )
如图所示,两个相互垂直的光滑绝缘固定挡板PO、OQ竖直放置在匀强电场E中,场强方向水平向左且垂直于挡板PO,图中A、B两球(可视为质点)质量相同且均带正电荷.当A球受竖直向下推力F作用时,A、B两球均紧靠挡板处于静止状态,这时两球之间的距离L;若使球A在推力F作用下沿挡板PO向O点移动一小段距离后,球A与球B重新处于静止状态,在此过程中( )| A. | A球对B球作用的静电力减小 | B. | A球对B球作用的静电力增大 | ||
| C. | 墙壁PO对A球的弹力不变 | D. | 两球之间的距离减小则F增大 |
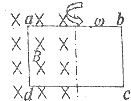 一个矩形线框在一个有界匀强磁场中绕对称轴以角速度ω匀速旋转,转轴恰与磁场的边界重合,如图所示,磁感应强度为B,线框的长边长为L,短边长为0.6L,线框总电阻为R,以线圈经过图示的位置开始计时,并规定电流方向沿a→b→c→d→a为正方向,试:
一个矩形线框在一个有界匀强磁场中绕对称轴以角速度ω匀速旋转,转轴恰与磁场的边界重合,如图所示,磁感应强度为B,线框的长边长为L,短边长为0.6L,线框总电阻为R,以线圈经过图示的位置开始计时,并规定电流方向沿a→b→c→d→a为正方向,试: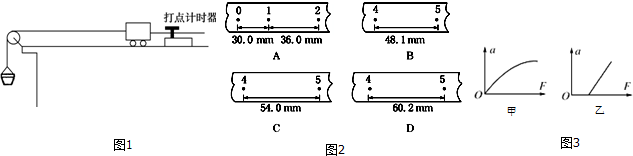
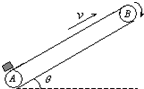 图示为一倾角θ=30°的传送带装置示意图,绷紧的传送带在A、B间始终保持v=1m/s的恒定速率向上运行,一个质量m=2kg的物体无初速地放在A处,传送带就将物体传送上去.设物体与传送带间的滑动摩擦力f=0.6mg,AB间的距离L=4m,g取10m/s2.求物体从A处传送到B处所需的时间t.
图示为一倾角θ=30°的传送带装置示意图,绷紧的传送带在A、B间始终保持v=1m/s的恒定速率向上运行,一个质量m=2kg的物体无初速地放在A处,传送带就将物体传送上去.设物体与传送带间的滑动摩擦力f=0.6mg,AB间的距离L=4m,g取10m/s2.求物体从A处传送到B处所需的时间t.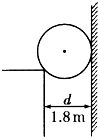 光滑圆球半径为1m,质量为6kg,静止于竖直墙壁与台阶之间图示位置,图中距离d为1.8m,求竖直墙壁和台阶对球的支持力分别为多大?(取g=10m/s2)
光滑圆球半径为1m,质量为6kg,静止于竖直墙壁与台阶之间图示位置,图中距离d为1.8m,求竖直墙壁和台阶对球的支持力分别为多大?(取g=10m/s2)