题目内容
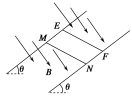
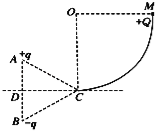
【题目】如图所示,竖直平面内![]() 光滑圆弧轨道半径为R,等边三角形ABC的边长为L,顶点C恰好位于圆周最低点,CD是AB边的中垂线.在A、B两顶点上放置一对等量异种电荷.现把质量为m带电荷量为+Q的小球由圆弧的最高点M处静止释放,到最低点C时速度为v0.不计+Q对原电场的影响,取无穷远处为零电势,静电力常量为k,则( )
光滑圆弧轨道半径为R,等边三角形ABC的边长为L,顶点C恰好位于圆周最低点,CD是AB边的中垂线.在A、B两顶点上放置一对等量异种电荷.现把质量为m带电荷量为+Q的小球由圆弧的最高点M处静止释放,到最低点C时速度为v0.不计+Q对原电场的影响,取无穷远处为零电势,静电力常量为k,则( )
A. 小球在圆弧轨道上运动过程机械能守恒
B. C点电势比D点电势高
C. M点电势为![]() (mv02﹣2mgR)
(mv02﹣2mgR)
D. 小球对轨道最低点C处的压力大小为mg+m![]() +2k
+2k![]()
【答案】C
【解析】
试题分析:此题属于电场力与重力场的复合场,根据机械能守恒和功能关系即可进行判断.
解:A、小球在圆弧轨道上运动重力做功,电场力也做功,不满足机械能守恒适用条件,故A错误;
B、CD处于AB两电荷的等势能面上,且两点的电势都为零,故B错误;
C、M点的电势等于![]() =
=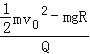 =
=![]() ,故C正确;
,故C正确;
D、小球对轨道最低点C处时,电场力为k![]() ,故对轨道的压力为mg+m
,故对轨道的压力为mg+m![]() +k
+k![]() ,故D错误;
,故D错误;
故选:C

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目