题目内容
(16分) 如图所示,生产车间有两个相互垂直且等高的水平传送带甲和乙,甲的速度为v0。小工件离开甲前与甲的速度相同,并平稳地传到乙上,工件与乙之间的动摩擦因数为μ,乙的宽度足够大,重力加速度为g。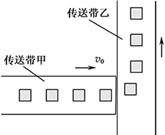
(1)若乙的速度为v0,求工件在乙上侧向(垂直于乙的运动方向)滑过的距离s;
(2)若乙的速度为2v0,求工件在乙上刚停止侧向滑动时的速度大小v;
(3)保持乙的速度2v0不变,当工件在乙上刚停止滑动时,下一只工件恰好传到乙上,如此反复。若每个工件的质量均为m,除工件与传送带之间摩擦外,其他能量损耗均不计,求驱动乙的电动机的平均输出功率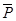 。
。
(1)s= ;(2)v=2v0;(3)
;(2)v=2v0;(3)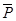 =
=
解析试题分析:(1)由于滑动摩擦力的方向与相等运动方向相反,因此首先应判断工件刚平稳地传到乙上瞬间,相对于传送带乙的运动方向,刚传到传送带乙上瞬间,工件有相对传送带乙侧向速度v0和与传送带乙运动方向相反的速度v0,其合速度方向与传送带运动方向显然成45°,如下图所示,并建立图示直角坐标系。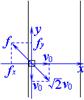
根据牛顿第二定律可知:ax=-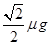 ,ay=
,ay=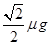
即物块相对传送带在沿传送带方向和垂直传送带方向分别做相同的匀减速直线运动,根据匀变速直线运动规律可知,当垂直传送带方向的速度减为零时,物块相对传送带在x方向上的位移即侧向滑过的距离为:s=
(2)同理作出工件相对传送带运动和所受滑动摩擦力的矢量图如下图所示。
设摩擦力与y轴方向间的夹角为θ,根据牛顿第二定律和加速度的定义式可知,始终存在: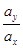 =
=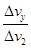 =tanθ=
=tanθ=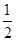
因此工件相对传送带做匀减速直线运动,因此工件在乙上刚停止侧向滑动时应相对传送带乙静止,因此工件此时的速度大小为:v=2v0
(3)每个工件在传送带乙上相对传送带滑行距离为:Δs=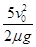
每个工件在传送带乙上相对传送带滑行的时间为:t=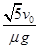
每个工件在相对传送带滑动的t时间内,电动机对乙做的功为:W=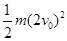 -
-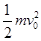 +μmgΔs
+μmgΔs
电动机的平均输出功率为: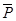 =
=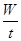
联立以上各式解得: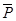 =
=
考点:本题主要考查了牛顿运动定律、滑动摩擦力的方向、运动的合成与分解的应用问题,属于较难题。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
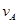 、
、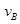 ;
;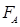 、
、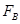 大小;
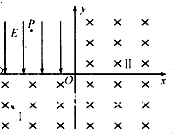
大小;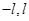 )点由静止释放,沿垂直于x轴的方向进入磁场I,接着以垂直于y轴的方向进入磁场Ⅱ,不计粒子重力.
)点由静止释放,沿垂直于x轴的方向进入磁场I,接着以垂直于y轴的方向进入磁场Ⅱ,不计粒子重力.