题目内容
19.在做“用单摆测定重力加速度”的实验过程中.
(1)某同学在做“用单摆测定重力加速度”的实验过程中,用毫米刻度尺测得摆线长L0=945.8mm;并用游标卡尺测得摆球的直径如图甲所示,则摆球直径d=20.30mm;用秒表测得单摆完成n=40次全振动的时间如图乙所示,则秒表的示数t=78.4s.
(2)如果该同学测得的g值偏小,可能的原因是AC.(填字母序号)
A.计算摆长时没有计入摆球的半径
B.开始计时时,秒表过迟按下
C.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
D.试验中误将39次全振动数为40次
(3)在“单摆测重力加速度”的实验中,如果摆球质量不均匀,按照正常的方法进行实验,会给测量结果造成误差.一个同学设计了一个巧妙的方法,可以避免上述误差,实验分两次进行,第一次测得悬线长为L1,测得振动周期为T1;第二次只改变悬线长为L2,并测得此时单摆的振动周期为T2,根据测量数据导出重力加速度的表达式为g=$\frac{4{π}^{2}({L}_{1}-{L}_{2})}{{T}_{1}^{2}-{T}_{2}^{2}}$.
分析 (1)游标卡尺读数规则为:先读主尺(只读整数),再加上游标尺(格数乘以分度分之一,格数找对齐的一个不估读);秒表读数等于大盘刻度读数加上小盘刻度读数;
(2)根据单摆周期公式列式分析即可;
(3)单摆的摆长应是悬点到摆球重心的距离,可假设摆线的结点到摆球重心距离为r,根据单摆的周期公式列式求出重力加速度的表达式.
解答 解:(1)主尺读数为:20mm,游标尺为20分度,精确度为0.05mm,读数为:6×0.05=0.30mm,故球的直径为:20mm+0.30mm=20.30mm;
秒表大盘读数18.4s,小盘读数60s,故秒表读数为:60s+18.4s=78.4s;
(2)同学测得的g值偏小,说明摆长测量值偏大或者周期测量值偏大;
A、计算摆长时没有计入摆球的半径,摆长测量值偏小,故加速度测量值偏小,故A正确;
B、开始计时时,秒表过迟按下,周期测量值偏小,故加速度测量值偏大,故B错误;
C、摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了,故相对与原来的单摆,周期测量值偏大了,故加速度测量值偏小,故C正确;
D、试验中误将39次全振动数为40次,周期测量值偏小,故加速度测量值偏大,故D错误;
故选:AC;
(3)设摆线的结点到摆球重心距离为r,则
T1=2π$\sqrt{\frac{{L}_{1}+r}{g}}$,
T2=2π$\sqrt{\frac{{L}_{2}+r}{g}}$
联立两式解得,g=$\frac{4{π}^{2}({L}_{1}-{L}_{2})}{{T}_{1}^{2}-{T}_{2}^{2}}$
故答案为:
(1)20.30;78.4;
(2)AC;(3)g=$\frac{4{π}^{2}({L}_{1}-{L}_{2})}{{T}_{1}^{2}-{T}_{2}^{2}}$.
点评 常用仪器的读数要掌握,这是物理实验的基础.掌握单摆的周期公式,从而求解加速度并进行误差分析.解决本题关键要抓住单摆的摆长与摆线长度之间的关系,运用单摆的周期公式进行解答.

 如图所示,固定在水平绝缘平面上足够长的金属导轨不计电阻,但表面粗糙,导轨左端连接一个电阻R,质量为m的金属棒(电阻也不计)放在导轨上,并与导轨垂直,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,用水平恒力F把ab棒从静止起向右拉动的过程中( )
如图所示,固定在水平绝缘平面上足够长的金属导轨不计电阻,但表面粗糙,导轨左端连接一个电阻R,质量为m的金属棒(电阻也不计)放在导轨上,并与导轨垂直,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,用水平恒力F把ab棒从静止起向右拉动的过程中( )| A. | 棒做匀加速运动 | |
| B. | 棒克服安培力做的功等于电路中产生的电能 | |
| C. | 恒力F和摩擦力的合力做的功等于电路中产生的电能和棒获得的动能之和 | |
| D. | 恒力F、摩擦力和安培力的合力做的功等于棒获得的动能 |
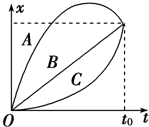
| A. | 在0~t0这段时间内,三质点位移关系为xA>xc>xB | |
| B. | 在t0时刻A、B、C运动方向相同 | |
| C. | 在0~t0这段时间内,三质点的平均速度相等 | |
| D. | B质点做匀加速直线运动,A、C加速度方向相反 |
 图为某同学探究物体加速度与合力、质量关系实验时,利用测量的数据绘出的a-F图象,根据图象可知( )
图为某同学探究物体加速度与合力、质量关系实验时,利用测量的数据绘出的a-F图象,根据图象可知( )| A. | 图1不过原点可能是没有平衡摩擦力 | |
| B. | 图2的物体质量大于图1对应的物体质量 | |
| C. | 图2不过原点一定是作图错误导致 | |
| D. | 图1线末端弯曲是因为改变拉力F时没有平衡摩擦力导致 |
| A. | 布朗运动的实质是液体分子的无规则运动 | |
| B. | 液体的沸点随大气压的增大而增大 | |
| C. | 在温度不变的条件下,饱和汽的体积减小,其压强增大 | |
| D. | 随着高科技的不断发展,绝对零度是可以达到的 | |
| E. | 热量不能自发从低温物体传给高温物体 | |
| F. | 将一个分子从无穷远处无限靠近另个分子,则分子力先增大后减小最后再增大 |
 甲、乙两人站在地面上时身材胖瘦都差不多0,乙站在地面处于静止状态、甲乘坐速度为0.8c(c为光速)的飞船向前运动,如图所示.此时甲观察到的乙身材比自身要瘦(填“胖”或“瘦”或“一样”)0;若乙在地面中吃了一顿饭时间为t0,甲观察到乙吃饭时间为t1,则t1>t0(均选填“>”、“=”或“<”).
甲、乙两人站在地面上时身材胖瘦都差不多0,乙站在地面处于静止状态、甲乘坐速度为0.8c(c为光速)的飞船向前运动,如图所示.此时甲观察到的乙身材比自身要瘦(填“胖”或“瘦”或“一样”)0;若乙在地面中吃了一顿饭时间为t0,甲观察到乙吃饭时间为t1,则t1>t0(均选填“>”、“=”或“<”).