Question

已知物体从地球上的逃逸速度(第二宇宙速度)v₂=,其中G、M、R分别是引力常量、地球的质量和半径.已知G=6.67×10^-11 N·m²/kg²,c=2.997 9×10⁸ m/s.求:

(1)逃逸速度大于真空中光速c的天体叫做黑洞,设某黑洞的质量等于太阳的质量1.98×10³⁰ kg.求它的可能最大半径(这个半径叫SchwarZchild半径);

(2)在目前天文观测范围内,物质的平均密度为10^-27 kg/m³.如果认为我们的宇宙是这样的一个均匀大球体,其密度使得它的逃逸速度大于光在真空中的光速c,因此任何物体都不脱离宇宙,问宇宙的半径至少多大?

Answer 1

解析：(1)由题目提供的地球的逃逸速度可以推知,任何天体(包括黑洞)均存在其对应的逃逸速度v₂=,其中G为引力常量,M、R分别为天体的质量和半径.对于黑洞模型,其逃逸速度大于真空中的光速c,即v₂=＞c

    所以其最大可能半径R＜

    将G=6.67×10^-11 N·m²/kg,M=1.98×10³⁰ kg,c=2.997 9×10⁸ m/s,代入上式计算得R=2.94×10³ m.

(2)把宇宙看作一个特殊的均匀大球体,设其密度为ρ,其半径为R,则其质量为M=ρ·πR³

    对应的逃逸速度为v₂=

    由于宇宙的密度ρ=10^-27 kg/m³,使得其逃逸速度大于光速c,即v₂＞c

    以上三式联立可得

    R＞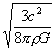

    =

    =4.01×10²⁶ m=4.24×10¹⁰光年.

    即宇宙的半径至少为4.24×10¹⁰光年.

答案：(1)2.94×10³ m

(2)4.24×10¹⁰光年