题目内容
已知物体从地球上的逃逸速度(第二宇宙速度)
解析:(1)把地球上第二宇宙速度的公式应用到黑洞上,则式中M、R为黑洞的质量和半径.
当逃逸速度等于光速时黑洞半径最大:![]() =2.93×
=2.93×
(2)同理,应用到宇宙这个假想的“均匀球体”上:
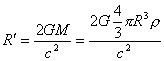 则:
则: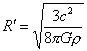
代入数据得:R′≈4.23×1010光年.

练习册系列答案
相关题目
题目内容
已知物体从地球上的逃逸速度(第二宇宙速度)
解析:(1)把地球上第二宇宙速度的公式应用到黑洞上,则式中M、R为黑洞的质量和半径.
当逃逸速度等于光速时黑洞半径最大:![]() =2.93×
=2.93×
(2)同理,应用到宇宙这个假想的“均匀球体”上:
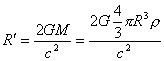 则:
则: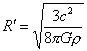
代入数据得:R′≈4.23×1010光年.
