题目内容
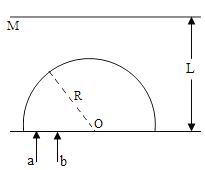
【题目】如图所示。在倾角为a=30。光滑斜面上,有一根长为L=0.8m的细绳,一端固定在O点,另一端系一质量为m=0.2kg的小球,沿斜面做圆周运动(g取10m/s2),试计算:

(1)小球通过最高点A的最小速度;
(2)若细绳抗拉力为FTmax=10N,小球在最低点B的最大速度是多少:
【答案】(1)2m/s(2)6m/s
【解析】试题分析:对小球进行受力分析,在最高点绳子拉力恰好为零时,速度取最小值,在最低点,合力提供向心力,根据向心力公式即可求解。
(1)小球通过最高点时,最小速度设为vA,
此时,小球重力沿斜面的力充当向心力:![]()
代入数据解得:vA=2m/s
(2)小球过最低点时,拉力向上,重力分力向下.
由牛顿第二定律:![]()
代入数据解得:vB=6m/s

练习册系列答案
相关题目