题目内容
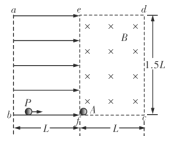
【题目】如图，光滑水平桌面上有一个矩形区域 abcd，bc长度为2L，cd长度为1.5L，e、f分别为ad、bc的中点。efcd区域存在竖直向下的匀强磁场，磁感应强度为B，质量为m、电荷量为+q的绝缘小球A静止在磁场中f点。abfe区域存在沿bf方向的匀强电场，电场强度为
，质量为km的不带电绝缘小球P，以大小为
的初速度沿bf方向运动。P与A发生弹性碰撞，A的电量保持不变，P、A均可视为质点。
(1)试求碰后A在磁场中做圆周运动的半径
(2)若k＝1，试分析A从ed边何处离开磁场:
(3)若A从ed边中点离开磁场，求k的可能值和A在磁场中运动的最长时间
【答案】（1）
；（2）
；（3）
；
【解析】
（1）P初速度
，设P、A碰后的速度分别为
和
，
由动量守恒定律：
由机械能守恒定律：
可得：
设A在磁场中运动轨迹半径为R，由牛顿第二定律：
可得
（2）当k=1时，R=L
如图1，易得离开磁场的点离e点距离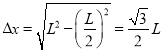
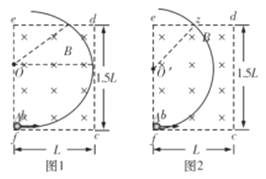
（3）令z点为ed边的中点，分类讨论如下：
（ⅰ）A球在磁场中偏转一次从z点就离开磁场，如图2有
解得：
由
可得：
（ⅱ）由图可知A球能从z点离开磁场要满足
，则A球在磁场中还可能经历一次半圆运动后回到电场，再被电场加速后又进入磁场，最终从z点离开。电场强度
；如图3和如图4，由几何关系有：
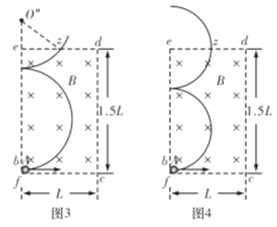
解得：
或
可得：
或
当时，
，由于
舍去
当时，
，由于
此类情形取符合题意要求，即
综合（ⅰ）、（ⅱ）可得A球能从z点离开的k的可能值为：或
A球在磁场中运动周期为
当时，如图4，A球在磁场中运动的最长时间
练习册系列答案
相关题目
