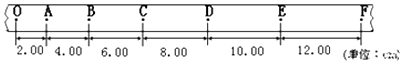��Ŀ����
����Ŀ����ͼ��ʾ��һ��������m=2kg��ƽ�峵��˷�������M=3kg��С���飬������ƽ�峵֮��Ķ�Ħ��������=0.4����ʼʱƽ�峵�ͻ��鹲ͬ��v0=2m/s���ٶ��ڹ⻬ˮƽ���������˶���������ֱǽ�ڷ�����ײ������ײʱ�伫������ײ��ƽ�峵�ٶȴ�С���ֲ��䣬��������ԭ���෴��ƽ�峵�㹻�����������鲻�Ử��ƽ�峵�Ҷˣ���ȡg=10m/s2����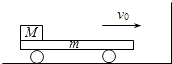
��1��ƽ�峵��һ����ǽ����ײ�������˶��������룮
��2��ƽ�峵�ڶ�����ǽ����ײǰ˲����ٶ�v��
��3��Ϊʹ����ʼ�ղ��Ử��ƽ�峵�Ҷˣ�ƽ�峵���ٶ��
���𰸡�
��1��
�⣺���һ����ǽ�ں�ƽ�峵�����ƶ�s���ٶ�Ϊ0��
����ϵͳ�ܶ������ң�ƽ�峵�ٶ�Ϊ��ʱ�����黹�����һ��У�
�ɶ��ܶ�����
����MgS=0�� ![]() m
m ![]() ��
��
s= ![]() ��
��
�������ݵ�s= ![]() m ��
m ��
��2��
�⣺����ƽ�峵�ڵڶ�����ײǰ��δ�ͻ�����Ծ�ֹ����ô���ٶȵĴ�С�϶�����2m/s��������ٶ������2m/s����������ң�������Υ�������غ㣮
����ƽ�峵�ڵڶ�����ײǰ�϶��Ѻͻ�����й�ͬ�ٶ�v���˼�ƽ�峵��ǽǰ˲����ٶȣ�
Mv0��mv0=��m+M��v ��
��v= ![]() v0 ��
v0 ��
�������ݵ�v= ![]() v0=0.4m/s ��
v0=0.4m/s ��
��3��
�⣺ƽ�峵��ǽ�ڷ��������ײ�����ͣ��ǽ�ߣ��軬�����ƽ�峵��λ��Ϊl��
���������غ����У�
![]() ��M+m��
��M+m�� ![]() =��Mgl ��
=��Mgl ��
l= ![]() ��
��
�������ݵ�l= ![]() m
m
l��Ϊƽ�峵����̳���
��������1��ϵͳ�ܶ������ң�ƽ�峵�ٶ�Ϊ��ʱ�����黹�����һ��У��ɶ��ܶ����г���ʽ���2������ƽ�峵�ڵڶ�����ײǰ��δ�ͻ�����Ծ�ֹ����Υ�������غ㣬����ƽ�峵�ڵڶ�����ײǰ�϶��Ѻͻ�����й�ͬ�ٶȣ����ݶ����غ㶨���г���ʽ���3�����������غ��г���ʽ���
�����㾫����������Ҫ�����˶����غ㶨�ɵ����֪ʶ�㣬��Ҫ���ն����غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��������ȷ�����⣮

 ��ʱ�ƿ�������ϰϵ�д�
��ʱ�ƿ�������ϰϵ�д� һ��һ��һ��ͨϵ�д�
һ��һ��һ��ͨϵ�д� �㽭֮��ѧҵˮƽ����ϵ�д�
�㽭֮��ѧҵˮƽ����ϵ�д�