题目内容
如图所示，在光滑的水平面上，质量分别为m和M（m：M=1：2）的物块A、B用轻质弹簧相连．当用水平恒力F作用于B上且两物块共同向右运动时，弹簧的伸长量为x1；当用同样大小的力F竖直匀加速提升两物块时，弹簧的伸长量为x2，则x1：x2等于（ ）分析：先对AB整体进行分析，可以得出整体运动的加速度；再对隔离出受力最少的一个进行受力分析，由牛顿第二定律可得出弹簧弹力，则可得出弹簧的形变量．
解答：解：由题意知，M=2m
水平面上，对整体有：F=（m+M）a1；=3ma1；
对A有：kx1=ma1
解得：x1=
在竖直面内，对整体有：F-3mg=3ma2；
对B分析有kx2-2mg=2ma2；
解得x2=
故x1：x2=1：2；
故B正确．
故选B．
水平面上，对整体有：F=（m+M）a1；=3ma1；
对A有：kx1=ma1
解得：x1=
| F |
| 3k |
在竖直面内，对整体有：F-3mg=3ma2；
对B分析有kx2-2mg=2ma2；
解得x2=
| 2F |
| 3K |
故x1：x2=1：2；
故B正确．
故选B．
点评：本题注意应用整体与隔离法，一般在用隔离法时优先从受力最少的物体开始分析，如果不能得出答案再分析其他物体；
本题中注意竖直面内时F作用的物体发生了变化，若F仍作用在B上，则形变量是不变的，可以通过分析得出结论．
本题中注意竖直面内时F作用的物体发生了变化，若F仍作用在B上，则形变量是不变的，可以通过分析得出结论．
练习册系列答案
相关题目
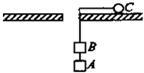如图所示，在光滑的水平板的中央有一光滑的小孔，用不可伸长的轻绳穿过小孔，绳的两端分别挂上小球C和物体B，在B的下端再挂一重物A，现使小球C在水平板上以小孔为圆心做匀速圆周运动，稳定时圆周运动的半径为R，现剪断连接A、B的绳子，稳定后，小球以另一半径在水平面上做匀速圆周运动，则下列说法正确的是（ ）
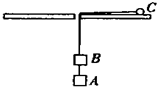如图所示，在光滑的水平板的中央有一光滑的小孔，一根不可伸长的轻绳穿过小孔．绳的两端分别拴有一小球C和一质量为m的物体B，在物体B的下端还悬挂有一质量为3m的物体A．使小球C在水平板上以小孔为圆心做匀速圆周运动，稳定时，圆周运动的半径为R．现剪断连接A、B的绳子，稳定后，小球以2R的半径在水平面上做匀速圆周运动，则下列说法正确的（ ）
如图所示，在光滑的水平板的中央有一光滑的小孔，用不可伸长的轻绳穿过小孔，绳的两端分别栓上一小球C和一物体B，在B的下端再悬挂一重物A，现使小球C在水平板上以小孔为圆心做匀速圆周运动，稳定时，圆周运动半径为R．现剪断连接AB的绳子，稳定后，小球以另一半径在水平面上做匀速圆周运动，则下列说法正确的是（ ）
