题目内容
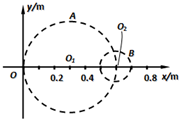 (2012?嘉兴二模)如图所示,在一平静水面上建立xOy坐标系,甲 乙两波源分别在O1 和O2位置先后以5Hz的频率上下振动,图中A、B为某一时刻两波刚到达的位置.波传播过程中能量损耗不计.图示时刻x=0.4m处的质点沿振动方向的位移为零,速度向下.已知水波的波速为0.5m/s,振幅为2cm,两波源起振方式相同,则下列说法正确的是( )
(2012?嘉兴二模)如图所示,在一平静水面上建立xOy坐标系,甲 乙两波源分别在O1 和O2位置先后以5Hz的频率上下振动,图中A、B为某一时刻两波刚到达的位置.波传播过程中能量损耗不计.图示时刻x=0.4m处的质点沿振动方向的位移为零,速度向下.已知水波的波速为0.5m/s,振幅为2cm,两波源起振方式相同,则下列说法正确的是( )分析:根据x=vt求出0.5s内波传播的距离,分析两波到达的位置;根据两波传播的距离,由公式x=vt确定出两波形成的时间,即可求解开始振动的时间关系;根据路程差,确定x=0.55m处质点振动强弱;根据图示时刻x=0.46m处的质点与A处振动关系,分析其振动方向.
解答:解;A、再经0.5s,两波传播的距离为x=vt=0.5×0.5m=0.25m,则甲波到达0.6m+0.25m=0.85m处,乙波到达0.7m+0.25m=0.95m处.故A错误.
B、两波已经形成的时间分别为t甲=
=
s=0.6s,t乙=
=
s=0.2s.故波源O1比O2开始振动的时间早0.4s.故B错误.
C、两波的波长为λ=
=0.1m,x=0.55m处到甲、乙两波源的路程差为△s=(0.55-0.3)-(0.6-0.55)=0.2m=2λ,故x轴上x=0.55m处发生干涉,振动始终加强.故C错误.
D、图示时刻x=0.46m处的质点与O1的距离为x=0.46m-0.3m=0.16m,而A处质点刚起振,速度方向向下,结合波形可知,x=0.46m处的质点振动方向向上.故D正确.
故选D
B、两波已经形成的时间分别为t甲=
| x甲 |
| v |
| 0.6-0.3 |
| 0.5 |
| x乙 |
| v |
| 0.1 |
| 0.5 |
C、两波的波长为λ=
| v |
| f |
D、图示时刻x=0.46m处的质点与O1的距离为x=0.46m-0.3m=0.16m,而A处质点刚起振,速度方向向下,结合波形可知,x=0.46m处的质点振动方向向上.故D正确.
故选D
点评:本题要抓住波在同一介质中匀速传播的特点,由x=vt求解时间,根据路程差,确定两波叠加后质点的振动情况.

练习册系列答案
相关题目
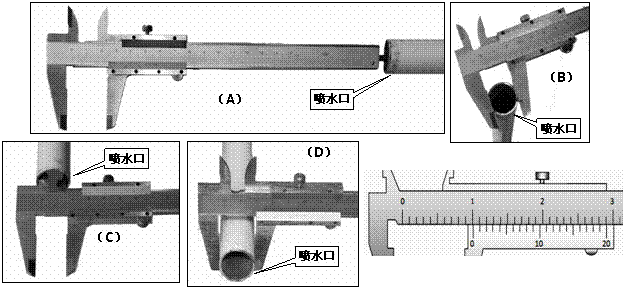
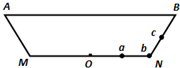 (2012?嘉兴二模)如图为某一水池的竖直截面,AB为水面,MN为水平池底,图中a、b、c为三个相同的发光点,位于N的发光点b发出的光恰能经水面全反射到达池底中央O点处,则( )
(2012?嘉兴二模)如图为某一水池的竖直截面,AB为水面,MN为水平池底,图中a、b、c为三个相同的发光点,位于N的发光点b发出的光恰能经水面全反射到达池底中央O点处,则( )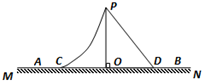 (2012?嘉兴二模)如图所示,曲面PC和斜面PD固定在水平面MN上,C、D处平滑连接,O点位于斜面顶点P的正下方.某人从顶端P由静止开始分别沿曲面和斜面滑下,经过C、D两点后继续运动,最后停在水平面的A、B两处.各处材质相同,忽略空气阻力,则( )
(2012?嘉兴二模)如图所示,曲面PC和斜面PD固定在水平面MN上,C、D处平滑连接,O点位于斜面顶点P的正下方.某人从顶端P由静止开始分别沿曲面和斜面滑下,经过C、D两点后继续运动,最后停在水平面的A、B两处.各处材质相同,忽略空气阻力,则( )