题目内容
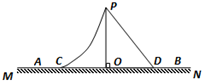（2012?嘉兴二模）如图所示，曲面PC和斜面PD固定在水平面MN上，C、D处平滑连接，O点位于斜面顶点P的正下方．某人从顶端P由静止开始分别沿曲面和斜面滑下，经过C、D两点后继续运动，最后停在水平面的A、B两处．各处材质相同，忽略空气阻力，则（ ）分析：将曲面分成无数小段，分别求出沿斜面PD下滑以及沿曲面下滑摩擦力做功，比较大小．根据全过程运用动能定理，比较全过程克服摩擦力做功．
解答：解：A、设PD斜面与水平方向上的夹角为θ，则PD段克服摩擦力做功Wf=μmgcosθs=μmgsPD水平．将PC段分成无数小段，由于在曲面上运动，径向的合力提供向心力，则支持力大于重力垂直于曲面方向上的分力，则每一小段克服摩擦力做功大于μmgscosα=μmgs水平，则整个曲面过程中，克服摩擦力做功大于μmgsPC水平．因为斜面和曲面的水平距离未知，则克服摩擦力做功不一定相等．故A错误．
B、对全过程运动动能定理得，mgh-Wf=0，知此人沿PCA和沿PDB运动克服摩擦力做功一定相等．故B错误．
C、因为整个过程克服摩擦力做功相等，沿斜面下滑在整个过程中摩擦力做功等于μmgsPB水平．而沿曲面下滑克服摩擦力做功大于μmgsPA水平，则OA一定小于OB．故C错误，D正确．
故选D．
B、对全过程运动动能定理得，mgh-Wf=0，知此人沿PCA和沿PDB运动克服摩擦力做功一定相等．故B错误．
C、因为整个过程克服摩擦力做功相等，沿斜面下滑在整个过程中摩擦力做功等于μmgsPB水平．而沿曲面下滑克服摩擦力做功大于μmgsPA水平，则OA一定小于OB．故C错误，D正确．
故选D．
点评：本题的难点是比较出μmgsPA水平与μmgsPB水平的大小关系，对曲面段采用微分思想．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
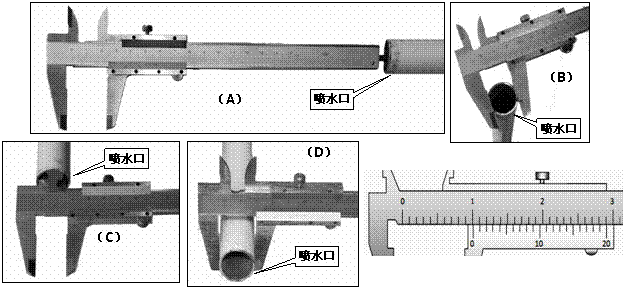
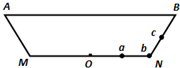（2012?嘉兴二模）如图为某一水池的竖直截面，AB为水面，MN为水平池底，图中a、b、c为三个相同的发光点，位于N的发光点b发出的光恰能经水面全反射到达池底中央O点处，则（ ）
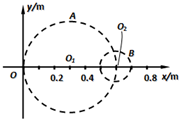（2012?嘉兴二模）如图所示，在一平静水面上建立xOy坐标系，甲 乙两波源分别在O1 和O2位置先后以5Hz的频率上下振动，图中A、B为某一时刻两波刚到达的位置．波传播过程中能量损耗不计．图示时刻x=0.4m处的质点沿振动方向的位移为零，速度向下．已知水波的波速为0.5m/s，振幅为2cm，两波源起振方式相同，则下列说法正确的是（ ）