题目内容
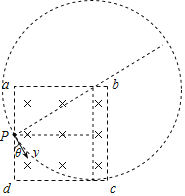
【题目】如图所示,边长为L的正方形abcd内有垂直于纸面向里、磁感应强度为B的匀强磁场,一束速率不同的带正电粒子从左边界ad中点P垂直射入磁场,速度方向与ad边夹角θ = 30°,已知粒子质量为m、电荷量为q,粒子间的相互作用和粒子重力不计.则( )

A. 粒子在磁场中运动的最长时间为![]()
B. 粒子在磁场中运动的最短时间为![]()
C. 上边界ab上有粒子到达的区域长为(1-![]() )L
)L
D. 下边界cd上有粒子到达的位置离c点的最短距离为![]()
【答案】AD
【解析】A项:粒子对应的圆心角越大,在磁场中运动的时间越长,最长时间对应的轨迹如图所示:
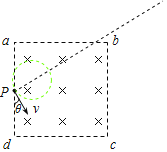
从pa边射出对应的轨迹的圆心角最大,为300°,故最长时间为:![]() ,故A正确;
,故A正确;
B项:考虑极限法,假设粒子速度无限大,则沿着直线穿过磁场,时间无穷小,故粒子在磁场中运动的最短时间趋向零,故B错误;
C项:画出临界轨迹,如图所示:

从ab边射出的最大的轨迹是与bc边相切,故:r1+r1sin60°=L,故![]() ,
,
从ab边射出的最小的轨迹是与ad边相切,故:![]() ,故
,故![]() ,
,
故上边界ab上有粒子到达的区域长为:![]() ,故C错误;
,故C错误;
D项:临界情况是轨迹与cd变相切,故:![]() ,解得r3=L,
,解得r3=L,
故下边界cd上有粒子到达的位置离c点的最短距离为![]() ,故D正确。
,故D正确。

练习册系列答案
相关题目