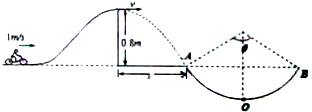
题目内容
如图所示,光滑曲面轨道置于高度为H=1.8m的平台上,其末端切线水平。另有一长木板两端分别搁在轨道末端点和水平地面间,构成倾角为θ=37°的斜面,整个装置固定在竖直平面内。一个可视作质点的质量为m=0.1kg的小球,从光滑曲面上由静止开始下滑(不计空气阻力,g取10m/s2,sin37°=0.6,cos37°=0.8)
(1)若小球从高h=0.45m处静止下滑,则小球离开平台时速度v0的大小是多少?
(2)若小球下滑后正好落在木板的末端,则释放小球的高度h为多大?
(3)试推导小球下滑后第一次撞击木板时的动能与它下滑高度h的关系表达式,并作出Ek-h图象。
(1)小球从曲面上滑下,只有重力做功,由机械能守恒定律:
mgh=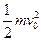 ① …(1分)
① …(1分) 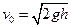
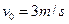 (1分)
(1分)
(2)小球离开平台后做平抛运动,小球正好落到水平地面木板的末端,则
H=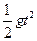 ②
② 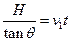 ③
③
联立②③式得: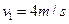 …(2分)
…(2分)
设释小球的高度为h1,则: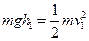
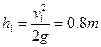 …(2分)
…(2分)
(3)由机械能守恒定律可得: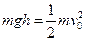
小球由离开平台后做平抛运动,可看做水平方向的匀速直线运动和竖直方向的自由落体运动,则: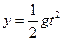 ④
④ 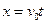 ⑤
⑤ 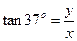 ⑥
⑥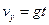 ⑦
⑦ 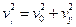 ⑧
⑧ 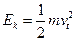 ⑨
⑨
由④⑤⑥⑦⑧⑨式得: Ek="3.25h " ⑩ ……(4分)
考虑到当h>0.8m时小球不会落到斜面上,其图象如图所示(2分)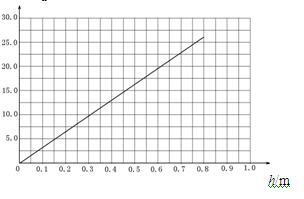
说明:图象描绘完整的给2分,不完整的给1分
解析

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 [物理]
[物理]