题目内容
 [物理]
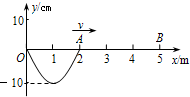
[物理]如图所示,摩托车做腾跃特技表演,以1m/s的初速度沿曲面冲上高0.8m顶部水平的高台,若摩托车冲上高台的过程中始终以额定功率1.8kW行驶,经过1.2s到达平台顶部.然后关闭发动机,离开平台,落至地面时,恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,并沿轨道下滑,A、B为圆弧两端点,其连线水平,已知圆弧半径为R=1.0m,已知人和车的总质量为180kg,特技表演的全过程中不计一切阻力.则:(计算中取g=10m/s2,sin53°=0.8,cos53°=0.6)
(1)求人和车从顶部平台飞出的水平距离s;
(2)人和车运动到圆弧轨道最低点O时对轨轨道的压力.
分析:(1)根据动能定理,求出人和摩托车到达平台顶端的速度,然后做平抛运动,根据高度求出平抛运动的时间,从而求出平抛运动的水平距离.
(4)摩托车恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,根据平抛运动的落地速度的方向求出圆弧的夹角,再结合动能定理和牛顿第二定律求出圆弧轨道对人和车的支持力大小,从而得出压力的大小.
(4)摩托车恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,根据平抛运动的落地速度的方向求出圆弧的夹角,再结合动能定理和牛顿第二定律求出圆弧轨道对人和车的支持力大小,从而得出压力的大小.
解答:解:(1)摩托车冲上高台的过程中,由动能定理得
Pt-mgh=
mv2-
mv02
代入数据解得:v=3m/s.
摩托车离开平台后做平抛运动过程中,在竖直方向上:
h=
gt2
代入数据解得t=0.4s.
水平方向上:s=vt=3×0.4m=1.2m.
(2)由于人和车无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,即人和车落到A点的速度方向沿A点切线方向.
vy=gt=4m/s.
由于人和车的水平速度为v=3m/s.
tanα=
=tan53°
摩托车由水平高台运动到圆弧轨道最低点的过程中,由动能定理得,
mv′2-
mv2=mg[h+R(1-cos53°)]
在最低点,由牛顿第二定律得:
FN-mg=m
代入数据解得FN=7740N
根据牛顿第三定律知,车对轨道的压力为7740N.
Pt-mgh=
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得:v=3m/s.
摩托车离开平台后做平抛运动过程中,在竖直方向上:
h=
| 1 |
| 2 |
代入数据解得t=0.4s.
水平方向上:s=vt=3×0.4m=1.2m.
(2)由于人和车无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,即人和车落到A点的速度方向沿A点切线方向.
vy=gt=4m/s.
由于人和车的水平速度为v=3m/s.
tanα=
| vy |
| v |
摩托车由水平高台运动到圆弧轨道最低点的过程中,由动能定理得,
| 1 |
| 2 |
| 1 |
| 2 |
在最低点,由牛顿第二定律得:
FN-mg=m
| v′2 |
| R |
代入数据解得FN=7740N
根据牛顿第三定律知,车对轨道的压力为7740N.
点评:本题涉及了不规则曲线运动、平抛运动和圆周运动,综合考查了动能定理和牛顿第二定律,综合性较强,对学生能力考查比较全面.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 A.(选修模块3-3)
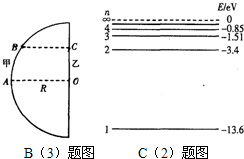
A.(选修模块3-3)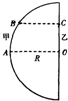 (3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少?
(3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少? 物理选修3-3
物理选修3-3 (2011?山东模拟)(物理-选修3-3):
(2011?山东模拟)(物理-选修3-3):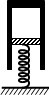 ,弹簧一端固定于水平面上,另一端与质量为m的活塞拴接在一起,开口向下、质量为M的气缸与活塞一起封闭了一定质量的气体.气缸和活塞均可与外界进行热交换.若外界环境的温度缓慢降低,则封闭气体的体积将
,弹簧一端固定于水平面上,另一端与质量为m的活塞拴接在一起,开口向下、质量为M的气缸与活塞一起封闭了一定质量的气体.气缸和活塞均可与外界进行热交换.若外界环境的温度缓慢降低,则封闭气体的体积将
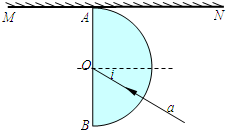
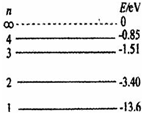
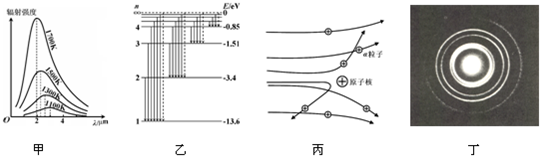
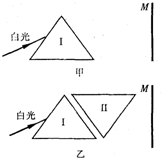 A、屏M自上而下分布的色光的波长由小到大
A、屏M自上而下分布的色光的波长由小到大