题目内容
[物理]
如图所示,摩托车做腾跃特技表演,以1m/s的初速度沿曲面冲上高0.8m顶部水平的高台,若摩托车冲上高台的过程中始终以额定功率1.8kW行驶,经过1.2s到达平台顶部.然后关闭发动机,离开平台,落至地面时,恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,并沿轨道下滑,A、B为圆弧两端点,其连线水平,已知圆弧半径为R=1.0m,已知人和车的总质量为180kg,特技表演的全过程中不计一切阻力.则:(计算中取g=10m/s2,sin53°=0.8,cos53°=0.6)
(1)求人和车从顶部平台飞出的水平距离s;
(2)人和车运动到圆弧轨道最低点O时对轨轨道的压力.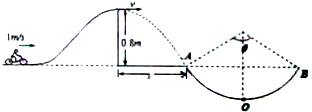
如图所示,摩托车做腾跃特技表演,以1m/s的初速度沿曲面冲上高0.8m顶部水平的高台,若摩托车冲上高台的过程中始终以额定功率1.8kW行驶,经过1.2s到达平台顶部.然后关闭发动机,离开平台,落至地面时,恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,并沿轨道下滑,A、B为圆弧两端点,其连线水平,已知圆弧半径为R=1.0m,已知人和车的总质量为180kg,特技表演的全过程中不计一切阻力.则:(计算中取g=10m/s2,sin53°=0.8,cos53°=0.6)
(1)求人和车从顶部平台飞出的水平距离s;
(2)人和车运动到圆弧轨道最低点O时对轨轨道的压力.

(1)摩托车冲上高台的过程中,由动能定理得
Pt-mgh=
mv2-
mv02
代入数据解得:v=3m/s.
摩托车离开平台后做平抛运动过程中,在竖直方向上:
h=
gt2
代入数据解得t=0.4s.
水平方向上:s=vt=3×0.4m=1.2m.
(2)由于人和车无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,即人和车落到A点的速度方向沿A点切线方向.
vy=gt=4m/s.
由于人和车的水平速度为v=3m/s.
tanα=
=tan53°
摩托车由水平高台运动到圆弧轨道最低点的过程中,由动能定理得,
mv′2-
mv2=mg[h+R(1-cos53°)]
在最低点,由牛顿第二定律得:
FN-mg=m
代入数据解得FN=7740N
根据牛顿第三定律知,车对轨道的压力为7740N.
Pt-mgh=
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得:v=3m/s.
摩托车离开平台后做平抛运动过程中,在竖直方向上:
h=
| 1 |
| 2 |
代入数据解得t=0.4s.
水平方向上:s=vt=3×0.4m=1.2m.
(2)由于人和车无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,即人和车落到A点的速度方向沿A点切线方向.
vy=gt=4m/s.
由于人和车的水平速度为v=3m/s.
tanα=
| vy |
| v |
摩托车由水平高台运动到圆弧轨道最低点的过程中,由动能定理得,
| 1 |
| 2 |
| 1 |
| 2 |
在最低点,由牛顿第二定律得:
FN-mg=m
| v′2 |
| R |
代入数据解得FN=7740N
根据牛顿第三定律知,车对轨道的压力为7740N.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 A.(选修模块3-3)
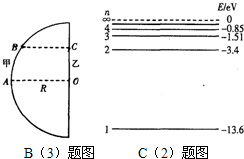
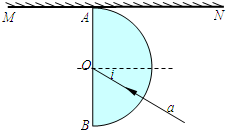
A.(选修模块3-3)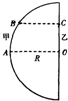 (3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少?
(3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少? 物理选修3-3
物理选修3-3 (2011?山东模拟)(物理-选修3-3):
(2011?山东模拟)(物理-选修3-3):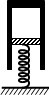 ,弹簧一端固定于水平面上,另一端与质量为m的活塞拴接在一起,开口向下、质量为M的气缸与活塞一起封闭了一定质量的气体.气缸和活塞均可与外界进行热交换.若外界环境的温度缓慢降低,则封闭气体的体积将
,弹簧一端固定于水平面上,另一端与质量为m的活塞拴接在一起,开口向下、质量为M的气缸与活塞一起封闭了一定质量的气体.气缸和活塞均可与外界进行热交换.若外界环境的温度缓慢降低,则封闭气体的体积将
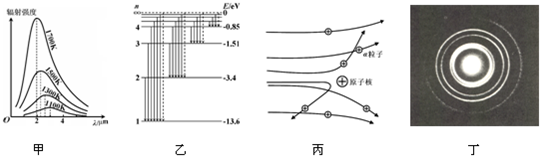
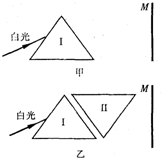 A、屏M自上而下分布的色光的波长由小到大
A、屏M自上而下分布的色光的波长由小到大