题目内容
2.已知引力常量G,某恒星半径R,一个环绕此恒星做匀速圆周运动的行星(运动只受恒星引力影响),距恒星表面的高度是h,行星绕恒星的运转周期T1,行星的自转周期T2,某同学根据以上条件,提出一种估算地球质量M的方法:行星绕恒星做圆周运动,由G$\frac{Mm}{{h}^{2}}$=mh$\frac{4{π}^{2}}{{{T}_{2}}^{2}}$得M=$\frac{4{π}^{2}{h}^{3}}{G{{T}_{2}}^{2}}$(1)请判断上面的结果是否正确,并说明理由,如不正确,请给出正确的解法和结果;
(2)恒星演化后期,部分恒星会因为内部引力而坍缩成为黑洞,根据拉普拉斯黑洞理论,黑洞的质量M和半径R的关系满足$\frac{M}{R}$=$\frac{{c}^{2}}{2G}$(其中c为光速,G为引力常量),假设题目中的恒星质量不变,则演化成黑洞的临界半径.
分析 (1)行星运转的轨道半径为R+h,结合行星绕恒星运转的周期,根据万有引力提供向心力求出恒星的质量.
(2)根据黑洞的质量M和半径R的关系满足$\frac{M}{R}$=$\frac{{c}^{2}}{2G}$,结合恒星的质量求出黑洞的临界半径.
解答 解:(1)错误.轨道半径和周期错误.
行星绕恒星做圆周运动,万有引力提供向心力.
$\begin{array}{l}G\frac{Mm}{{{{(R+h)}^2}}}=m\frac{{4{π^2}}}{{{T_1}^2}}(R+h)\\ M=\frac{{4{π^2}}}{{G{T_1}^2}}{(R+h)^3}\end{array}$
(2)由题意可知,最小半径$R=\frac{2GM}{c^2}=\frac{{8{π^2}}}{{{c^2}{T_1}^2}}{(R+h)^3}$.
答:(1)解法错误,轨道半径和周期错误,地球质量M为$\frac{4{π}^{2}}{G{{T}_{1}}^{2}}(R+h)^{3}$.
(2)演化成黑洞的临界半径为$\frac{8{π}^{2}}{{c}^{2}{{T}_{1}}^{2}}(R+h)^{3}$.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,注意高度和轨道半径的不同,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.一定质量的理想气体,在温度不变条件下,设法使其压强增大,则这一过程( )
| A. | 气体的密度增加 | B. | 气体分子的平均动能增大 | ||
| C. | 外界没有对气体做功 | D. | 气体从外界吸收了热量 |
10.对于一定量的理想气体,下列说法正确的是( )
| A. | 若气体的压强不变,分子每秒对器壁单位面积平均碰撞次数随温度升高而减小 | |
| B. | 若气体的内能不变,其状态也一定不变 | |
| C. | 若气体的体积不变则压强跟温度一定成正比 | |
| D. | 气体温度每升高1 K所吸收的热量与气体经历的过程有关 |
7.关于加速度,下列说法正确的是( )
| A. | 物体的速度变化量大,加速度就一定大 | |
| B. | 物体运动的时间越长,加速度就一定越来越小 | |
| C. | 物体可能做加速度减小的加速运动 | |
| D. | 物体具有的加速度向东,所以它不可能向西运动 |
14.关于经典力学和相对论、量子力学,下列说法正确的是( )
| A. | 不论是对宏观物体,还是微观粒子,经典力学和量子力学都是适用的 | |
| B. | 经典力学适用于低速运动的物体,相对论适用于高速运动的物体 | |
| C. | 经典力学适用于宏观物体的运动,量子力学适用于微观粒子的运动 | |
| D. | 相对论与量子力学否定了经典力学理论 |
12.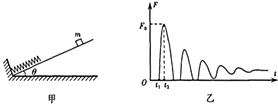 如图甲,固定斜面倾角为θ,底部挡板连一轻质弹簧.质量为m的物块从斜面上某一高度处静止释放,不断撞击弹簧,最终静止.物块所受弹簧弹力F的大小随时间t变化的关系如图乙,物块与斜面间的动摩擦因数为μ,弹簧在弹性限度内,重力加速度为g,则( )
如图甲,固定斜面倾角为θ,底部挡板连一轻质弹簧.质量为m的物块从斜面上某一高度处静止释放,不断撞击弹簧,最终静止.物块所受弹簧弹力F的大小随时间t变化的关系如图乙,物块与斜面间的动摩擦因数为μ,弹簧在弹性限度内,重力加速度为g,则( )
 如图甲,固定斜面倾角为θ,底部挡板连一轻质弹簧.质量为m的物块从斜面上某一高度处静止释放,不断撞击弹簧,最终静止.物块所受弹簧弹力F的大小随时间t变化的关系如图乙,物块与斜面间的动摩擦因数为μ,弹簧在弹性限度内,重力加速度为g,则( )
如图甲,固定斜面倾角为θ,底部挡板连一轻质弹簧.质量为m的物块从斜面上某一高度处静止释放,不断撞击弹簧,最终静止.物块所受弹簧弹力F的大小随时间t变化的关系如图乙,物块与斜面间的动摩擦因数为μ,弹簧在弹性限度内,重力加速度为g,则( )| A. | 物块运动过程中,物块和弹簧组成的系统机械能守恒 | |
| B. | 物块运动过程中,t1到t2某时刻速度最大 | |
| C. | 物块运动过程中的最大加速度大小为$\frac{{F}_{0}-mgsinθ+μmgcosθ}{m}$ | |
| D. | 最终静止时,物块受到的重力、斜面支持力和摩擦力的合力方向沿斜面向上 |
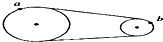 在如图所示的皮带传动装置中,a是大轮边缘上的一点,b是小轮边缘上的一点.当皮带轮匀速转动时,皮带与轮间不打滑.a、b两点的线速度的大小是va=vb(选填“>”、“=”或“<”);a、b两点的角速度的大小是ωa<ωb(选填“>”、“=”或“<”).
在如图所示的皮带传动装置中,a是大轮边缘上的一点,b是小轮边缘上的一点.当皮带轮匀速转动时,皮带与轮间不打滑.a、b两点的线速度的大小是va=vb(选填“>”、“=”或“<”);a、b两点的角速度的大小是ωa<ωb(选填“>”、“=”或“<”). “研究平抛运动”实验中,在印有小方格纸上记下小球在空中运动的一系列位置 a、b、c、d,如图所示.已知图中小方格边长的实际长度为L,则小球水平抛出时的初速度v0=$2\sqrt{gL}$(用重力加速度g、边长L表示).
“研究平抛运动”实验中,在印有小方格纸上记下小球在空中运动的一系列位置 a、b、c、d,如图所示.已知图中小方格边长的实际长度为L,则小球水平抛出时的初速度v0=$2\sqrt{gL}$(用重力加速度g、边长L表示).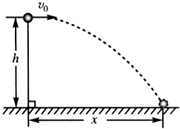 如图所示,将一个小球水平抛出,抛出点距水平地面的高度h=1.8m,小球抛出的初速度为v0=8m/s.不计空气阻力.取g=10m/s2.求:
如图所示,将一个小球水平抛出,抛出点距水平地面的高度h=1.8m,小球抛出的初速度为v0=8m/s.不计空气阻力.取g=10m/s2.求: