题目内容
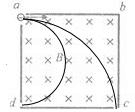
 (2010?厦门二模)如图所示,将截面为正方形的真空腔abcd放置在一匀强磁场中,磁场方向垂直纸面向里.若有一束具有不同速率的电子由小孔a沿ab方向射入磁场,打在腔壁上的被吸收,则关于由小孔c和小孔d射出的电子的时间比值和运动速率比值正确的是( )
(2010?厦门二模)如图所示,将截面为正方形的真空腔abcd放置在一匀强磁场中,磁场方向垂直纸面向里.若有一束具有不同速率的电子由小孔a沿ab方向射入磁场,打在腔壁上的被吸收,则关于由小孔c和小孔d射出的电子的时间比值和运动速率比值正确的是( )分析:带电粒子在磁场中做圆周运动,由几何知识可分别求得从c点和d点飞出的粒子的半径,则由向心力公式可求得各自的速率及比值;由转动的角度可知运动时间之比.
解答:解:设磁场边长为a,如图所示,粒子从c点离开,其半径为a;
A、B:粒子的运行周期:T=
;
从图可得,从c点离开的粒子运行的时间是
个周期:tC=
从d点离开的粒子运行的时间是半个周期:tD=
T;
故
=
=
.故A错误,B错误;
C、D:由洛伦兹力提供向心力得:BqvC=
可得:vC=
;
粒子从d点离开,其半径为
;
同理可得:vD=
故
=
; 故C错误,D正确.
故选:D.

A、B:粒子的运行周期:T=
| 2πm |
| qB |
从图可得,从c点离开的粒子运行的时间是
| 1 |
| 4 |
| T |
| 4 |
从d点离开的粒子运行的时间是半个周期:tD=
| 1 |
| 2 |
故
| tC |
| tD |
| ||
|
| 1 |
| 2 |
C、D:由洛伦兹力提供向心力得:BqvC=
m
| ||
| a |
可得:vC=
| Bqa |
| m |
粒子从d点离开,其半径为
| a |
| 2 |
同理可得:vD=
| Bqa |
| 2m |
故
| vC |
| vD |
| 2 |
| 1 |
故选:D.
点评:本题属于带电粒子在磁场中的偏转中典型题目,此类题的关键在于确定圆心及由几何关系求出半径.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目

 (2010?厦门二模)如图所示,一束红光从空气垂直射到直角玻璃三棱镜的界面AB上,棱镜材料对红光的折射率为
(2010?厦门二模)如图所示,一束红光从空气垂直射到直角玻璃三棱镜的界面AB上,棱镜材料对红光的折射率为 (2010?厦门二模)我国未来将建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭动力的航天飞机在月球引力作用下经椭圆轨道向月球靠近,并将与空间站在B处对接.已知空间站绕月轨道半径为r,周期为T,万有引力常量为G,下列说法中正确的是( )
(2010?厦门二模)我国未来将建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭动力的航天飞机在月球引力作用下经椭圆轨道向月球靠近,并将与空间站在B处对接.已知空间站绕月轨道半径为r,周期为T,万有引力常量为G,下列说法中正确的是( ) (2010?厦门二模)如图所示,A、B两球完全相同,质量为m,用两根等长的细线悬挂在O点,两球之间夹着一根劲度系数为k的轻弹簧,静止不动时,弹簧位于水平方向,两根细线之间的夹角为θ.则弹簧的长度被压缩了( )
(2010?厦门二模)如图所示,A、B两球完全相同,质量为m,用两根等长的细线悬挂在O点,两球之间夹着一根劲度系数为k的轻弹簧,静止不动时,弹簧位于水平方向,两根细线之间的夹角为θ.则弹簧的长度被压缩了( )