题目内容
 (2010?厦门二模)如图所示,A、B两球完全相同,质量为m,用两根等长的细线悬挂在O点,两球之间夹着一根劲度系数为k的轻弹簧,静止不动时,弹簧位于水平方向,两根细线之间的夹角为θ.则弹簧的长度被压缩了( )
(2010?厦门二模)如图所示,A、B两球完全相同,质量为m,用两根等长的细线悬挂在O点,两球之间夹着一根劲度系数为k的轻弹簧,静止不动时,弹簧位于水平方向,两根细线之间的夹角为θ.则弹簧的长度被压缩了( )分析:对A球受力分析,然后根据平衡条件并运用合成法得到弹簧的弹力,最后根据胡克定律得到弹簧的压缩量.
解答:解:对球A受力分析,受重力mg、拉力T、弹簧的弹力F,如图
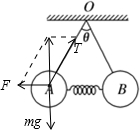
根据平衡条件,结合合成法,有:
F=mgtan
根据胡克定律,有:
F=kx
解得:x=
故选:A.

根据平衡条件,结合合成法,有:
F=mgtan
| θ |
| 2 |
根据胡克定律,有:
F=kx
解得:x=
mgtan
| ||
| k |
故选:A.
点评:本题关键是对小球受力分析,然后根据共点力平衡条件并运用合成法求解出弹力,最后根据胡克定律求解出弹簧的压缩量.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目

 (2010?厦门二模)如图所示,一束红光从空气垂直射到直角玻璃三棱镜的界面AB上,棱镜材料对红光的折射率为
(2010?厦门二模)如图所示,一束红光从空气垂直射到直角玻璃三棱镜的界面AB上,棱镜材料对红光的折射率为 (2010?厦门二模)我国未来将建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭动力的航天飞机在月球引力作用下经椭圆轨道向月球靠近,并将与空间站在B处对接.已知空间站绕月轨道半径为r,周期为T,万有引力常量为G,下列说法中正确的是( )
(2010?厦门二模)我国未来将建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭动力的航天飞机在月球引力作用下经椭圆轨道向月球靠近,并将与空间站在B处对接.已知空间站绕月轨道半径为r,周期为T,万有引力常量为G,下列说法中正确的是( ) (2010?厦门二模)如图所示,将截面为正方形的真空腔abcd放置在一匀强磁场中,磁场方向垂直纸面向里.若有一束具有不同速率的电子由小孔a沿ab方向射入磁场,打在腔壁上的被吸收,则关于由小孔c和小孔d射出的电子的时间比值和运动速率比值正确的是( )
(2010?厦门二模)如图所示,将截面为正方形的真空腔abcd放置在一匀强磁场中,磁场方向垂直纸面向里.若有一束具有不同速率的电子由小孔a沿ab方向射入磁场,打在腔壁上的被吸收,则关于由小孔c和小孔d射出的电子的时间比值和运动速率比值正确的是( )