��Ŀ����
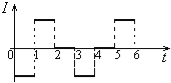
����Ŀ����ͼ��ʾ������r=0.3��������m=0.1kg�Ľ�����CD��ֱ������λ��ˮƽ���ϵ�����ƽ�й⻬���������ϣ��������뵼���Ӵ����ã�������費�ƣ�������˽�����ֵR=0.5���ĵ��衣����Ϊ0��3.0A�ĵ�����������һ�������ϣ�����Ϊ0��1.0V�ĵ�ѹ�����ڵ���R�����ˡ���ֱ����ƽ�����ǿ�ų����´���ƽ�档�������Һ㶨����Fʹ�����������ƶ����۲쵽������ʾ������������ʾ���ȶ�������һ�����������ƫ������һ�����δ��ƫ����ʱ��������ٶ�Ϊv=2m/s���������Ϊ����������

��1������������������F���
��2������������ȶ���ijһʱ�̣���ȥ����F����˺����R�ϲ����������Ƕ��٣�
��3���ڣ�2���������£������ͨ������R�ĵ����ܹ�Ϊ0.25���أ���˺�����˶�����λ�ƶ��
���𰸡���1��1.6N��2��0.125J��3��0.25
����������1����CD�˲����ĵ綯��ΪE����������ʾ��ΪI�����R�о�����֪�� ![]()
�������ĸ�Ӧ�綯��Ϊ E=BLv
�ɱպϵ�·ŷķ�����У� ![]() ���ã�
���ã� ![]()
��CD���ܵ�������ΪF����������С FA=BIL=0.8��2N=1.6N
��Ϊ�ȶ�ʱ�������˶�������F=FA=1.6N
��2���������غ㣬��·�в����ĵ���Q����CD�����ܵļ�����![]() mv2��Q
mv2��Q
�ã�Q=![]() ��0.1��22J=0.2J
��0.1��22J=0.2J
����R�ϲ����ĵ���![]()
��3���赼����˶�����λ��Ϊs������![]()
![]()
![]()
![]()
�������s=0.25m