��Ŀ����
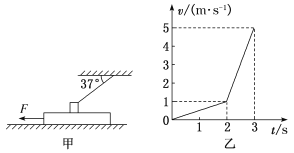
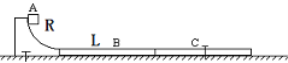
����Ŀ����ͼʾ������������ͬ������A��B��C������ľ��B��C��ȫ��ͬ�����ȶ�ΪL��ˮƽ����⻬�����Կ����ʵ������A�Ӱ뾶ΪR��![]() �̶��⻬Բ������ˣ����ٻ��£����ϵ�ľ��B��Բ���ĩ��ˮƽ���뾲ֹľ��ȸߣ��������ٶ�Ϊg����һ��ľ��C���ö��ӹ̶��ڵ����ϣ�A���Ϻ�պ�δ����B���ͣ�£��ù�������ʱ��Ϊt1����������ΪQ1���ڶ���Cľ�屻�ſ���A��ͬ�����ٳ���B��ֱ�������ȶ����ù�������ʱ��Ϊt2����������ΪQ2��t1��t2��Q1��Q2δ֪������
�̶��⻬Բ������ˣ����ٻ��£����ϵ�ľ��B��Բ���ĩ��ˮƽ���뾲ֹľ��ȸߣ��������ٶ�Ϊg����һ��ľ��C���ö��ӹ̶��ڵ����ϣ�A���Ϻ�պ�δ����B���ͣ�£��ù�������ʱ��Ϊt1����������ΪQ1���ڶ���Cľ�屻�ſ���A��ͬ�����ٳ���B��ֱ�������ȶ����ù�������ʱ��Ϊt2����������ΪQ2��t1��t2��Q1��Q2δ֪������
(1)С���A��ľ��֮��Ķ�Ħ��������=��
(2)ǰ����������ʱ��ı�ֵ![]() =��
=��
(3)ǰ�����β�������֮��ֵ![]() =��
=��
���𰸡�(1)![]() ��(2)
��(2)![]() ��(3)
��(3)![]()
��������
(1)��һ��C�̶�����A�ö��ܶ�����
![]()
�ɵ�
![]()
(2)A�ļ��ٶ�Ϊ
![]()
��A����B�ij��ٶ�Ϊ![]() ������
������
![]()
��A��B��C�ö����غ㶨�ɵ�
![]()
�ɵ�
![]()
��B��C��ţ�ٵڶ����ɵ�
![]()
������������
![]()
�ɵ�ǰ����������ʱ��ı�ֵ
![]()
(3)��һ��ľ��C���ö��ӹ̶��ڵ����ϣ��ù��̲�������Ϊ![]() ����A�ö��ܶ�����
����A�ö��ܶ�����
![]()
�ڶ���Cľ�屻�ſ������������غ�ɵ�
![]()
��������ֵΪ
![]()

��ϰ��ϵ�д�
 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д�
�����Ŀ