题目内容
12.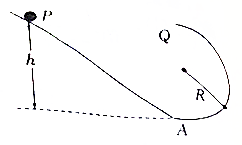 如图,PAQ是一个固定的光滑轨道,其中PA是直线部分,AQ是半径为R的半圆弧,PA与AQ相切,P、Q两点在同一水平高度.现有一小球自P点由静止开始沿轨道下滑.那么( )
如图,PAQ是一个固定的光滑轨道,其中PA是直线部分,AQ是半径为R的半圆弧,PA与AQ相切,P、Q两点在同一水平高度.现有一小球自P点由静止开始沿轨道下滑.那么( )| A. | 小球不可能到达Q点,P比Q至少高$\frac{R}{2}$才能经Q点沿切线方向飞出 | |
| B. | 小球能到达Q点,到达后,又沿原轨道返回 | |
| C. | 小球能到达Q点,到达后,将自由下落 | |
| D. | 小球能到达Q点,到达后,恰能沿圆弧的切线方向飞出 |
分析 小球恰好到达Q点时由重力提供向心力,由牛顿第二定律求Q点的临界速度,再由机械能守恒求出P与Q间的最小高度.即可作出判断.
解答 解:小球恰好到达Q点时由重力提供向心力,由牛顿第二定律得:mg=m$\frac{{v}_{Q}^{2}}{R}$
可得Q点的临界速度为 vQ=$\sqrt{gR}$
设小球恰好到达Q点时P与Q高h,则由机械能守恒定律得
mg(h-2R)=$\frac{1}{2}m{v}_{Q}^{2}$
解得 h=$\frac{5}{2}$R
可知,小球不可能到达Q点,P比Q至少高$\frac{R}{2}$才能经Q点沿切线方向飞出,故A正确,BCD错误.
故选:A.
点评 解决本题的关键要掌握竖直平面内圆周运动的临界条件:小球恰好到达Q点时由重力提供向心力,由牛顿第二定律和机械能守恒定律结合解答.

练习册系列答案
相关题目
2.关于磁通量,下列说法中正确的是( )
| A. | 磁通量是标量 | |
| B. | 磁通量越大,磁感应强度越大 | |
| C. | 通过某一平面的磁通量为零,该处磁感应强度不一定为零 | |
| D. | 磁通量就是磁感应强度 |
3.测量一个未知电阻Rx的阻值,用多用电表的欧姆挡粗测未知电阻,采用“×10”挡,调零后测量该电阻,发现指针偏转非常大,最后几乎紧挨满偏刻度停下来,下列判断和做法正确的是 ( )
| A. | 这个电阻很小,估计只有几欧姆 | |
| B. | 这个电阻很大,估计有几千欧姆 | |
| C. | 如需进一步测量可换“×1”挡,调零后测量 | |
| D. | 如需进一步测量可换“×1k”挡,调零后测量 |
20.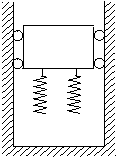 如图一升降机在箱底装有若干个弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦力,则升降机在从弹簧下端触地后直到最低点的一段运动过程中( )
如图一升降机在箱底装有若干个弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦力,则升降机在从弹簧下端触地后直到最低点的一段运动过程中( )
 如图一升降机在箱底装有若干个弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦力,则升降机在从弹簧下端触地后直到最低点的一段运动过程中( )
如图一升降机在箱底装有若干个弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦力,则升降机在从弹簧下端触地后直到最低点的一段运动过程中( )| A. | 升降机的速度不断减小 | |
| B. | 升降机的加速度不断变大 | |
| C. | 先是弹力做的负功小于重力做的正功,然后是弹力做的负功大于重力做的正功 | |
| D. | 到最低点时,升降机加速度的值一定大于重力加速度的值 |
4.下列哪些现象属于能量的耗散( )
| A. | 利用水流能发电产生电能 | B. | 电能在灯泡中变成光能 | ||
| C. | 电池的化学能变成电能 | D. | 火炉把屋子烤暖 |
14. 如图所示,匀强电场中有一圆,其所在平面与电场线平行,O为圆心,A、B、C、D为圆周上的四个等分点.若将某带电粒子从A点以相同的初动能向各个不同的方向发射,到达圆周上各点时,过D点动能最大,不计重力和空气阻力.则( )
如图所示,匀强电场中有一圆,其所在平面与电场线平行,O为圆心,A、B、C、D为圆周上的四个等分点.若将某带电粒子从A点以相同的初动能向各个不同的方向发射,到达圆周上各点时,过D点动能最大,不计重力和空气阻力.则( )
 如图所示,匀强电场中有一圆,其所在平面与电场线平行,O为圆心,A、B、C、D为圆周上的四个等分点.若将某带电粒子从A点以相同的初动能向各个不同的方向发射,到达圆周上各点时,过D点动能最大,不计重力和空气阻力.则( )
如图所示,匀强电场中有一圆,其所在平面与电场线平行,O为圆心,A、B、C、D为圆周上的四个等分点.若将某带电粒子从A点以相同的初动能向各个不同的方向发射,到达圆周上各点时,过D点动能最大,不计重力和空气阻力.则( )| A. | 该电场的电场线一定与OD平行 | |
| B. | 该带电粒子一定带正电 | |
| C. | 带电粒子若经过C点,则其动能不可能与初动能相同 | |
| D. | 带电粒子不可能经过B点 |
 如图所示,质量为m的物体与A,B两个弹簧相连,B弹簧下端与地相连,其劲度系数分别为k1和k2,现用手拉A的上端,使A缓慢上移,当B弹簧的弹力为原来的$\frac{1}{3}$时,A的上端移动的距离是多少?
如图所示,质量为m的物体与A,B两个弹簧相连,B弹簧下端与地相连,其劲度系数分别为k1和k2,现用手拉A的上端,使A缓慢上移,当B弹簧的弹力为原来的$\frac{1}{3}$时,A的上端移动的距离是多少?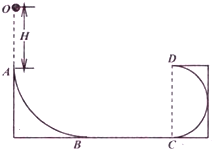 如图,ABCD轨道固定在竖直平面内,AB是半径R1=1m的四分之一圆弧轨道,与水平面相切与B点,CD是半径R2=0.5m光滑半圆轨道,与水平面相切与C点,BC段动摩擦因数μ=0.3.现一可视为质点的小球,从距离A点正上方高H=2m的O点静止释放后,恰沿A点进入轨道,通过B点时的速度为7m/s,已知小球质量m=0.2kg,不计空气阻力,g=10m/s2求:
如图,ABCD轨道固定在竖直平面内,AB是半径R1=1m的四分之一圆弧轨道,与水平面相切与B点,CD是半径R2=0.5m光滑半圆轨道,与水平面相切与C点,BC段动摩擦因数μ=0.3.现一可视为质点的小球,从距离A点正上方高H=2m的O点静止释放后,恰沿A点进入轨道,通过B点时的速度为7m/s,已知小球质量m=0.2kg,不计空气阻力,g=10m/s2求: