题目内容
17. 如图所示,质量为m的物体与A,B两个弹簧相连,B弹簧下端与地相连,其劲度系数分别为k1和k2,现用手拉A的上端,使A缓慢上移,当B弹簧的弹力为原来的$\frac{1}{3}$时,A的上端移动的距离是多少?
如图所示,质量为m的物体与A,B两个弹簧相连,B弹簧下端与地相连,其劲度系数分别为k1和k2,现用手拉A的上端,使A缓慢上移,当B弹簧的弹力为原来的$\frac{1}{3}$时,A的上端移动的距离是多少?
分析 题中要求弹簧B产生的弹力大小变成原来的$\frac{1}{3}$,此时B弹簧有两种可能的状态:拉伸和压缩.B原来处于压缩状态,后来处于拉伸或压缩状态,根据胡克定律分别求出B原来压缩量和后来的伸长量或压缩量,即可得到M上移的距离.再根据胡克定律求出甲的伸长量,加上M上移的距离就是A端上移的距离.
解答 解:B弹簧原先处于压缩状态,压缩量为:x1=$\frac{Mg}{{k}_{2}}$,甲弹簧无形变.
情况一:用手拉住弹簧A的上端,缓慢上移时,B弹簧仍处于压缩状态,压缩量:
x2=$\frac{Mg}{3{k}_{2}}$;
则物体M上升的距离为:
S1=x1-x2=$\frac{Mg}{{k}_{2}}$-$\frac{Mg}{3{k}_{2}}$=$\frac{2Mg}{3{k}_{2}}$;
由M受力平衡可知,甲弹簧处于拉伸状态,伸长量:
x3=$\frac{2Mg}{3{k}_{1}}$
则A的上端应上移为:l1=S1+x3=$\frac{2Mg}{3{k}_{2}}$+$\frac{2Mg}{3{k}_{1}}$=$\frac{2Mg({k}_{1}+{k}_{2})}{3{k}_{1}{k}_{2}}$;
情况二:用手拉住弹簧A的上端,缓慢上移时,B弹簧处于拉伸状态,伸长量:
x2=$\frac{Mg}{3{k}_{2}}$;
则物体M上升的距离为:
S2=x1+x2=$\frac{Mg}{3{k}_{2}}$+$\frac{Mg}{{k}_{2}}$=$\frac{4Mg}{3{k}_{2}}$
由M受力平衡可知,A弹簧处于拉伸状态,形变量:
x4=$\frac{4Mg}{3{k}_{1}}$
则A的上端应上移:
l2=S2+x4=$\frac{4Mg}{3{k}_{2}}$+$\frac{4Mg}{3{k}_{1}}$=4$\frac{{K}_{1}+{K}_{2}}{3{K}_{1}{K}_{2}}$Mg
答:A的上端移动的距离是$\frac{2Mg({k}_{1}+{k}_{2})}{3{k}_{1}{k}_{2}}$或4$\frac{{K}_{1}+{K}_{2}}{3{K}_{1}{K}_{2}}$Mg
点评 本题的解题关键是分析弹簧的状态,分析出A端上移的距离与弹簧形变量的关系,要注意不能漏解.

| A. | 位移和路程总是大小相等,但位移是矢量,路程是标量 | |
| B. | 研究飞行中直升飞机上的螺旋桨的转动性能时可以将其看成质点 | |
| C. | 时间就是一段长时间,时刻就是一段短时间 | |
| D. | 速度变化越来越慢,就是加速度越来越小 |
 如图所示的皮带传动装置中,M、N分别是两个轮边缘的质点,两皮带轮半径分别为r和R,且r=$\frac{2}{3}$R,则( )
如图所示的皮带传动装置中,M、N分别是两个轮边缘的质点,两皮带轮半径分别为r和R,且r=$\frac{2}{3}$R,则( )| A. | M、N角速度之比为3:2 | B. | M、N线速度大小之比为3:2 | ||
| C. | M、N向心加速度之比为1:1 | D. | 以上说法都不正确 |
| A. | 磁感线可以形象的描述磁场的强弱与方向 | |
| B. | 磁感线越密的地方磁场强度越强,越疏的地方磁场强度越弱 | |
| C. | 磁感线都是从N极出发,终止于S极 | |
| D. | 磁感线与电场线一样都不能相交 |
 如图,PAQ是一个固定的光滑轨道,其中PA是直线部分,AQ是半径为R的半圆弧,PA与AQ相切,P、Q两点在同一水平高度.现有一小球自P点由静止开始沿轨道下滑.那么( )
如图,PAQ是一个固定的光滑轨道,其中PA是直线部分,AQ是半径为R的半圆弧,PA与AQ相切,P、Q两点在同一水平高度.现有一小球自P点由静止开始沿轨道下滑.那么( )| A. | 小球不可能到达Q点,P比Q至少高$\frac{R}{2}$才能经Q点沿切线方向飞出 | |
| B. | 小球能到达Q点,到达后,又沿原轨道返回 | |
| C. | 小球能到达Q点,到达后,将自由下落 | |
| D. | 小球能到达Q点,到达后,恰能沿圆弧的切线方向飞出 |
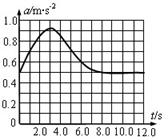 某研究性学习小组用加速度传感器探究物体从静止开始做直线运动的规律,得到了质量为1.0kg的物体运动的加速度随时间变化的关系图线,如图所示.由图可以得出( )
某研究性学习小组用加速度传感器探究物体从静止开始做直线运动的规律,得到了质量为1.0kg的物体运动的加速度随时间变化的关系图线,如图所示.由图可以得出( )| A. | 从t=4.0s到t=6.0s的时间内物体做匀减速直线运动 | |
| B. | 从t=2.0s到t=6.0s的时间内物体所受合外力保持不变 | |
| C. | 在t=10.0s时的速度大小约为6.8m/s | |
| D. | 从t=10.0s到t=12.0s的时间内合外力对物体做的功约为7.3J |
 (1)一个多用电表的原理电路如图1所示,电流计G的量程Ig=0.001A,内阻Rg=100Ω,R1=9900Ω,R2=1.01Ω.
(1)一个多用电表的原理电路如图1所示,电流计G的量程Ig=0.001A,内阻Rg=100Ω,R1=9900Ω,R2=1.01Ω.①若要当做电流表使用,双刀双掷电键应与cd连接(选填“ab”或“cd“),其量程为0-0.1A.
②若要当做电压表使用,双刀双掷电键应与ab连接(选填“ab”或“cd”),其量程为0-10V.
(2)现有一刻度均匀、量程未准确确定的电压表V1,已知其量程在13-16V之间,内阻r1=150kΩ.为测定其准确量程,实验室提供了如表所列的器材,要求方法简洁,尽可能减少误差,并能测出多组数据.
| 器材(代号) | 规格 |
| 标准电压表V2 | 量程3V,内阻r2=30kΩ |
| 电流表A | 量程3A,内阻r3=0.01Ω |
| 滑动变阻器R | 总阻值1kΩ |
| 稳压电源E | 20V,内阻很小 |
| 开关S、导线若干 |
②根据测量效果最好的那个电路图,将图3有关器材连接成测量电路.
| A. | 秒表 | B. | 天平 | C. | 弹簧秤 | D. | 重锤线 |