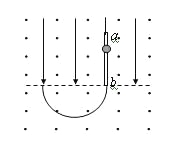
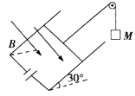
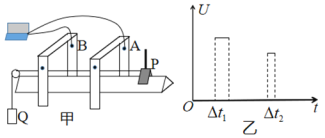
[题目]如图所示.空间中存在水平向右的匀强电场E＝8×103V/m.带电量q＝1×10-6C.质量m＝1×10-3kg的小物块固定在水平轨道的O点.AB为光滑固定的圆弧轨道.半径R＝0.4m.物块由静止释放.冲上圆弧轨道后.最终落在C点.已知物块与OA轨道间的动摩擦因数为＝0.1.OA＝R.重力加速度g＝10m/s2.求:(1)物块在A点的速度大小vA(结果题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示，空间中存在水平向右的匀强电场E＝8×103V/m，带电量q＝1×10—6C、质量m＝1×10—3kg的小物块固定在水平轨道的O点，AB为光滑固定的圆弧轨道，半径R＝0.4m。物块由静止释放，冲上圆弧轨道后，最终落在C点，已知物块与OA轨道间的动摩擦因数为＝0.1，OA＝R，重力加速度g＝10m/s2，求:

(1)物块在A点的速度大小vA(结果可保留根号)

(2)物块到达B点时对轨道的压力

(3)OC的距离(结果可保留根号)。

【答案】(1)(2)(3)

【解析】

(1)对物块从O到A由动能定理得

代入数据解得

(2)对小物块从O到B点由动能定理得

在B点由牛顿第二定律得

联立解得

(3)对小物块从O到B点由动能定理得

解得

离开B点后竖直方向先做匀减速运动，上升到最高点离B点高度为

所用的时间为

从最高点落到地面的时间为

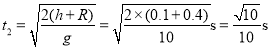
则B到C的水平距离为

所以OC的距离

练习册系列答案

相关题目

【题目】如图所示，虚线上方有场强为E的匀强电场，方向竖直向下，虚线上下有磁感应强度相同的匀强磁场，方向垂直纸面向外，ab是一根长为L的绝缘细杆，沿电场线放置在虚线上方的场中，b端在虚线上.将一套在杆上的带正电的小球从a端由静止释放后，小球先做加速运动，后做匀速运动到达b端。已知小球与绝缘杆间的动摩擦因数μ=0.3，小球重力忽略不计，当小球脱离杆进入虚线下方后，运动轨迹是半圆，圆的半径是L/3，求带电小球从a到b运动过程中克服摩擦力所做的功与电场力所做功的比值。

【题目】在“测定金属的电阻率”的实验中，某同学所测的金属导体的形状如图甲所示，其横截面为空心的等边三角形，外等边三角形的边长是内等边三角形边长的2倍，内三角形为中空。

为了合理选用器材设计测量电路，他先用多用表的欧姆挡“×1”按正确的操作步骤粗测其电阻，指针如图乙，则读数应记为________ Ω。

现利用实验室的下列器材，精确测量它的电阻R，以便进一步测出该材料的电阻率ρ：

A．电源E(电动势为3 V，内阻约为1 Ω)

B．电流表A1(量程为0～0.6 A，内阻r1 约为1 Ω)

C．电流表A2(量程为0～0.6 A，内阻r2＝5 Ω)

D．最大阻值为10 Ω的滑动变阻器R0

E．开关S，导线若干

(1)请在图丙虚线框内补充画出完整、合理的测量电路图_______________。

(2)先将R0调至最大，闭合开关S，调节滑动变阻器R0，记下各电表读数，再改变R0进行多次测量。在所测得的数据中选一组数据，用测量量和已知量来计算R时，若A1的示数为I1，A2的示数为I2，则该金属导体的电阻 R＝________。

(3)该同学用直尺测量导体的长度为L，用螺旋测微器测量了外三角形的边长a。测边长a时，螺旋测微器读数如图丁所示，则a＝________ mm。用已经测得的物理量I1、I2、L、a及题中所给物理量可得到该金属材料电阻率的表达式为ρ＝________。

【题目】某国际天文研究小组观测到了一组双星系统，它们绕二者连线上的某点做匀速圆周运动，双星系统中质量较小的星体能“吸食”质量较大的星体的表面物质，达到质量转移的目的．根据大爆炸宇宙学可知，双星间的距离在缓慢增大，假设星体的轨道近似为圆，则在该过程中(　　)

A. 双星做圆周运动的角速度不断减小

B. 双星做圆周运动的角速度不断增大

C. 质量较大的星体做圆周运动的轨道半径减小

D. 质量较大的星体做圆周运动的轨道半径增大

【答案】AD

【解析】试题分析：双星绕两者连线的一点做匀速圆周运动，由相互之间万有引力提供向心力，根据万有引力定律、牛顿第二定律和向心力进行分析．

解：AB、设体积较小的星体质量为m1，轨道半径为r1，体积大的星体质量为m2，轨道半径为r2．双星间的距离为L．转移的质量为△m．

根据万有引力提供向心力对m1：=（m1+△m）ω2r1… ①

对m2：=（m2﹣△m）ω2r2… ②

由①②得：ω=，总质量m1+m2不变，两者距离L增大，则角速度ω变小．故A正确、B错误．

CD、由②式可得，把ω的值代入得：，

因为，L增大，故r2增大．即质量较大的星体做圆周运动的轨道半径增大，故C错误、D正确．

故选：AD．

【点评】本题是双星问题，要抓住双星系统的条件：角速度与周期相同，运用牛顿第二定律采用隔离法进行研究．

【题型】单选题
【结束】
38

【题目】如图所示，一匀强电场的电场线平行于xOy平面，电场强度大小为E，xOy平面上有一椭圆，椭圆的长轴在x轴上，E、F两点为椭圆的两个焦点，AB是椭圆的短轴，椭圆的一端过O点，则下列说法正确的是(　　)

A. 在椭圆上，O、C两点间电势差一定最大

B. 在椭圆上，A、B两点间电势差可能最大

C. 一个点电荷从E点运动到椭圆上任意一点再运动到F点，电场力做功可能为零

D. 一个点电荷从O点运动到A点与从B点运动到C点，电场力做功一定相同

【题目】如图所示，两平行光滑金属导轨与水平面的夹角为30°，导轨一端接有电源，电源电动势为，内阻为Ω，导轨宽度为，导轨间横跨一根电阻为Ω的导体棒，棒的质量为，棒系在轻绳的一端，另一端绕过定滑轮悬挂一个质量为的物块，匀强磁场垂直于导轨所在平面向下，已知导轨电阻可忽略不计，滑轮左侧轻绳与导轨平行，重力加速度。

（1）若释放导体棒后，棒保持静止状态，则磁感应强度B为多大?

（2）若磁感应强度，则释放导体棒瞬间，轻绳的拉力为多大?

【题目】如图所示，电阻不计、间距为l的光滑平行金属导轨水平放置于磁感应强度为B、方向竖直向下的匀强磁场中，导轨左端接一定值电阻R。质量为m、电阻为r的金属棒MN置于导轨上，受到垂直于金属棒的水平外力F的作用由静止开始运动，外力F与金属棒速度v的关系是F=F0+kv（F0、k是常量），金属棒与导轨始终垂直且接触良好。金属棒中感应电流为i，受到的安培力大小为FA，电阻R两端的电压为UR，感应电流的功率为P，它们随时间t变化图象可能正确的有

A. B.

C. D.

【题目】如图所示，在平行于水平地面的有理想边界的匀强磁场上方，有三个大小相同的，且用相同的金属材料制成的正方形线框，线框平面与磁场方向垂直。A线框有一个缺口，B、C线框都闭合，但B线框导线的横截面积比C线框大。现将三个线框从同一高度由静止开始同时释放，下列关于它们落地时间说法正确的是（　　）

A.三个线框同时落地

B.三个线框中，A线框最早落地

C.B线框在C线框之后落地

D.B线框和C线框在A线框之后同时落地

【题目】某研究性学习小组利用气垫导轨验证机械能守恒定律，实验装置如图甲所示。在气垫导轨上相隔一定距离的两处安装两个光电传感器A、B，滑块P上固定一遮光条，若光线被遮光条遮挡，光电传感器会输出高电压，两光电传感器采集数据后与计算机相连。滑块在细线的牵引下向左加速运动，遮光条经过光电传感器A、B时，通过计算机可以得到如图乙所示的电压U随时间t变化的图像。

（1）实验前，接通气源，将滑块（不挂钩码）至于气垫导轨上，轻推滑块，当图乙中的t1_______t2(选填“大于”、“等于”或“小于”)时，说明气垫导轨已调水平。

（2）用螺旋测微器测遮光条宽度d，测量结果如图丙所示，则d=________mm。

（3）滑块P用细线绕过气垫导轨左端的定滑轮与质量为m的钩码Q相连，将滑块P由图甲所示位置释放，通过计算机得到的图像如图乙所示，若t1、t2、m、g和d已知，若已测出滑块质量M ，两光电门间距离L。上述物理量间满足关系式_______________，则表明在上述过程中，滑块和砝码组成的系统机械能守恒。

【题目】一质点做匀速直线运动。现对其施加一恒力，且原来作用在质点上的力不发生改变，则（）

A. 质点速度的方向总与该恒力的方向相同

B. 质点加速度的方向总与该恒力的方向相反

C. 质点可能先做匀减速运动再做匀加速运动，但最小速度不为0

D. 质点单位时间内速率的变化量总是不变

试题分类