题目内容
 (2012?上海模拟)在一次国际城市运动会中,要求运动员从高为H=4m的平台上A点由静止出发,沿着动摩擦因数为μ=0.2的滑道向下运动到B点后水平滑出,最后落在水池中.滑道的水平距离L大小不变,设滑道的水平距离为L=5m,B点的高度h可由运动员自由调节,A点不动,AB长度可以调整.(取g=10m/s2) 求:
(2012?上海模拟)在一次国际城市运动会中,要求运动员从高为H=4m的平台上A点由静止出发,沿着动摩擦因数为μ=0.2的滑道向下运动到B点后水平滑出,最后落在水池中.滑道的水平距离L大小不变,设滑道的水平距离为L=5m,B点的高度h可由运动员自由调节,A点不动,AB长度可以调整.(取g=10m/s2) 求:(1)运动员要达到最大水平运动距离,B点的高度h应调为多大?平抛过程的最大水平距离Smax为多少?
(2)为了研究物体从B点沿光滑抛物线轨道顶端无初速下滑的运动,制做一个与第(1)中运动员平抛轨迹完全相同的光滑轨道,并将该轨道固定在与BC曲线重合的位置,让另一物体P沿该轨道无初速下滑(下滑过程中始终不会脱离轨道),则物体P通过轨道最低点C时的水平分速度和竖直分速度大小.
分析:(1)运动员在滑道上有重力和摩擦力做功,由动能定理可求得运动员到达B点的速度;离开滑道后,运动员做平抛运动,由平抛运动的规律求出水平距离与初速度的关系,联立得出水平距离与h的关系式,运用数学知识求得出最大水平距离及B的高度.
(2)对于物体离开B点做平抛运动的过程,由运动学公式求得在C点水平速度和竖直速度的方向与实际速度方向夹角.物体P从B到C的过程中满足机械能守恒定律,根据题意,轨迹相同,在任意点它们的速度方向相同,根据机械能守恒列式,即可求解.
(2)对于物体离开B点做平抛运动的过程,由运动学公式求得在C点水平速度和竖直速度的方向与实际速度方向夹角.物体P从B到C的过程中满足机械能守恒定律,根据题意,轨迹相同,在任意点它们的速度方向相同,根据机械能守恒列式,即可求解.
解答:解:(1)设斜面长度为L1,斜面倾角为α,由A运动到B过程,根据动能定理得:
mg(H-h)-μmg?L1cosα=
m
-0
解得v0=
平抛运动过程:s=v0t,
h=
gt2
解得 s=2
=2
当h=-
=
(H-μL)=1.5m时,s有最大值,Smax=3m.
(2)对BC运动轨迹:y=
gt2,t=
s,
所以落到C点时的竖直分速度大小是vy=
m/s.
又因水平分速度大小为vB=v0=
m/s,所以物体在C点水平速度和竖直速度的方向与实际速度方向夹角都是45° 角.
物体P从B到C的过程中满足机械能守恒定律,mgh=
mvc2,得vc=
m/s,
因轨迹相同,所以在任意点它们的速度方向相同,所以到C点后水平分速度和竖直分速度的大小是
vx=vy=
vc=
m/s
答:
(1)运动员要达到最大水平运动距离,B点的高度h应调为1.5m,平抛过程的最大水平距离Smax为3m.
(2)物体P通过轨道最低点C时的水平分速度和竖直分速度大小都是
m/s.
mg(H-h)-μmg?L1cosα=
| 1 |
| 2 |
| v | 2 0 |
解得v0=
| 2g(H-h-μL) |
平抛运动过程:s=v0t,
h=
| 1 |
| 2 |
解得 s=2
| (H-μL-h)h |
| -h2+(H-μL)h |
当h=-
| H-μL |
| 2×(-1) |
| 1 |
| 2 |
(2)对BC运动轨迹:y=
| 1 |
| 2 |
| 0.3 |
所以落到C点时的竖直分速度大小是vy=
| 30 |
又因水平分速度大小为vB=v0=
| 30 |
物体P从B到C的过程中满足机械能守恒定律,mgh=
| 1 |
| 2 |
| 30 |
因轨迹相同,所以在任意点它们的速度方向相同,所以到C点后水平分速度和竖直分速度的大小是
vx=vy=
| ||
| 2 |
| 15 |
答:
(1)运动员要达到最大水平运动距离,B点的高度h应调为1.5m,平抛过程的最大水平距离Smax为3m.
(2)物体P通过轨道最低点C时的水平分速度和竖直分速度大小都是
| 15 |
点评:物体在恒力作用下可由动能定理求解,难点在于数学知识的应用,平时学习中要注意数学知识的积累和解题能力的培养.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
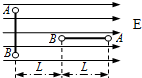 (2012?上海模拟)如图所示,绝缘杆两端固定带电小球A和B,轻杆处于水平向右的匀强电场中,不考虑两球之间的相互作用.初始时杆与电场线垂直,将杆右移的同时顺时针转过90°,发现A、B两球电势能之和不变.根据如图给出的位置关系,下列说法正确的是( )
(2012?上海模拟)如图所示,绝缘杆两端固定带电小球A和B,轻杆处于水平向右的匀强电场中,不考虑两球之间的相互作用.初始时杆与电场线垂直,将杆右移的同时顺时针转过90°,发现A、B两球电势能之和不变.根据如图给出的位置关系,下列说法正确的是( )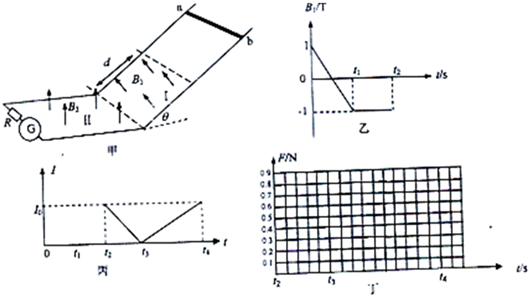
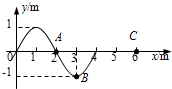 (2012?上海模拟)一列沿x正方向传播的简谐波t=0时刻的波形如图所示,t=0.2s时C点开始振动,则( )
(2012?上海模拟)一列沿x正方向传播的简谐波t=0时刻的波形如图所示,t=0.2s时C点开始振动,则( )