题目内容
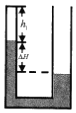
【题目】如图所示,U形管左管截面半径为r1,右管截面半径![]() 倍,设右管足够高,管内水银在左管内封闭了一段长为h1=19cm,温度为T1=240K的空气柱,左右两管水银面高度差为ΔH=16cm,大气压为P0=76cmHg.现向右管缓慢补充水银,保持左管内气体的温度不变。直到左右两边水银面相平时,求:
倍,设右管足够高,管内水银在左管内封闭了一段长为h1=19cm,温度为T1=240K的空气柱,左右两管水银面高度差为ΔH=16cm,大气压为P0=76cmHg.现向右管缓慢补充水银,保持左管内气体的温度不变。直到左右两边水银面相平时,求:
(1)此时气柱的长度最终结果保留两位有效数字
(2)对封闭气体加热,则其重新回到19cm的长度时,封闭气体温度T为多少K?
【答案】(1)15(2)328K
【解析】
解:![]() 设水银的密度为
设水银的密度为![]() ,U型管左右两边横截面积分别为
,U型管左右两边横截面积分别为![]() ,
,![]() ,封闭气体依次在三种状态下的压强分别为
,封闭气体依次在三种状态下的压强分别为![]() 、
、![]() 、
、![]()
![]()
解得:![]()
两边液面相平时,封闭气体压强为:![]() ,封闭气体长度为
,封闭气体长度为![]()
该过程为等温过程,由波意耳定律有:![]()
解得:![]()
![]() 封闭气体回到原长度时,右管比左管液面高出
封闭气体回到原长度时,右管比左管液面高出![]()
![]()
与初态相比,是等容过程,由查理定律得:![]()
解得:![]()
答:![]() 此时气柱的长度为15cm;
此时气柱的长度为15cm;
![]() 对封闭气体加热,则其重新回到19cm的长度时,封闭气体温度T为328K。
对封闭气体加热,则其重新回到19cm的长度时,封闭气体温度T为328K。

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目