Question

【题目】竖直平面内的四个光滑轨道，由直轨道和平滑连接的圆弧轨道组成，圆轨道的半径为R ，P 为圆弧轨道的最低点。P 点左侧的四个轨道均相同，P 点右侧的四个圆弧轨道的形状如图所示。现让四个相同的小球 （ 可视为质点，直径小于图丁中圆管内径 ） 分别从四个直轨道上高度均为h 处由静止下滑，关于小球通过P 点后的运动情况，下列说法正确的是 （ ）

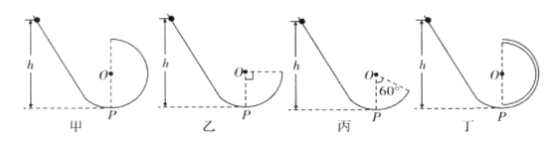
A.若 h＜R，则四个小球能达到的最大高度均相同

B.若 h=R ，则四个小球能达到的最大高度均相同

C.若h=R ，则图乙中的小球能达到的高度最大

D.若 h=R ，则图甲、图丙中的小球能达到的最大高度相同

Answer 1

【答案】ACD

【解析】

A．若，根据机械能守恒定律可知，四个小球都能上升到右侧高度处，即小球不会超过圆弧的四分之一轨道，则不会脱离圆轨道，故上升到最高点的速度均位列零，最大高度相同为h，A正确；

B．若h＝R，根据机械能守恒，甲乙丁都能上升到右侧高度R处而不会越过圆弧的四分之一轨道，而丙图中小球做斜上抛运动离开轨道，到达最高点时还有水平的速度，最大高度小于R，B错误；

C．若，甲、丁两图中的小球不会脱离圆轨道，最高点的速度不为零，丙图小球离开轨道，最高点速度也不为零，乙图离开轨道，上升到最高点的速度为零，根据机械能守恒知，图乙中小球到达的高度最大，故C正确；

D．若，图甲中小球到达的最大高度为2R，根据机械能守恒得，

得最高点的速度为

对于图丙，设小球离开轨道时的速度为v1，根据机械能守恒得，

而到达最高点的速度

v=v1cos60°，

联立解得最高点的速度

则两球到达最高点的速度相等，根据机械能守恒得，甲、丙图中小球到达的最大高度相等，故D正确；

故选ACD。