Question

【题目】2009年7月22日，在我国长江流域的广大区域，都看到了时间长达5分多钟的日全食，其中武汉市是这次日全食很接近月影中心的大城市。这次武汉日全食的具体时间是：初亏8时14分54秒；食既9时23分58秒；食甚9时26分41秒；生光9时29分22秒；复圆10时46分06秒。全食时间共5分24秒，食分为1.075（即以太阳视直径为1，食甚时刻太阳直径被月亮遮挡的为1.075）。

还已知：月球的直径约为地球直径的1/3.8，太阳离地球的距离约为月球离地球距离的400倍。月球绕地球公转周期约27.3天，转动方向为自西向东。地球半径R=6.4×103km。武汉的纬度约为31。7月22日是夏至后的一个月，这时太阳直射北纬20.5 附近。（sin31=0.52. cos31=0.86, sin10=0.17. cos10=0.98）

试根据以上信息，估算此次日全食过程中，武汉地区日食带的宽度（即在武汉附近能看到日全食的地区南北方向的宽度）。（结果要求保留两位有效数字）

Answer 1

【答案】2.0×102 km。

【解析】

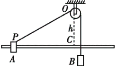
解法1：作如图所示的示意图，图中O1、O2分别表示月球和太阳的中心，O是地球上月影的中心。O1A表示月球的半径（O1A=R/3.8），O2B表示太阳的半径。

连接OB交O1A于A1，则

则AA1=0.0184R, B1B=400 AA1

连接BA并延长，交过O点的OO2的垂线于C，则OC就是地球上月球影子（本影）的半径，由几何关系知

OC＝≈AA1=0.0184R=1.2 ×102km

月球本影的直径为2OC≈2.4×102 km

考虑到7月22日太阳直射北纬21 附近，而武汉位于北纬31，全食带的宽度应除以cos（31 -21）, 即全食带的宽度为2OC /cos（31 -21 ） ≈2.4×102 km。

解法2：月球绕地球公转，周期为27.3天，半径为地球半径的60倍，其线速度

km/s＝1.022 km/s，

假设地球不自转，月球在地面上的影子的移动速度

武汉地面观察者随地球自转的线速度

km/s＝0.400 km/s

日全食经历的时间 t＝5ˊ24"=324s

月球本影东西方向的直径为

D=（v月影-v武汉）t=（1.022-0.400）×324 km≈2.0×102 km

考虑到7月22日太阳直射北纬21 附近，而武汉位于北纬31，全食带的宽度应除以cos（31 -21）, 即全食带的宽度为D /cos（31 -21 ） ≈2.0×102 km。