题目内容
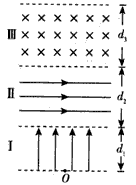
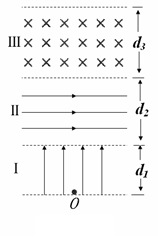
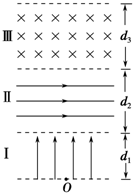 如图所示空间分为Ⅰ,Ⅱ,Ⅲ三个足够长的区域,各边界面相互平行,其中Ⅰ,Ⅱ区域存在匀强电场EI=1.0×104 V/m,方向垂直边界面竖直向上;EⅡ=×105 V/m,方向水平向右,Ⅲ区域磁感应强度B=5.0T,方向垂直纸面向里,三个区域宽度分别为d1=5.0m,d2=4.0m,d3=10
如图所示空间分为Ⅰ,Ⅱ,Ⅲ三个足够长的区域,各边界面相互平行,其中Ⅰ,Ⅱ区域存在匀强电场EI=1.0×104 V/m,方向垂直边界面竖直向上;EⅡ=×105 V/m,方向水平向右,Ⅲ区域磁感应强度B=5.0T,方向垂直纸面向里,三个区域宽度分别为d1=5.0m,d2=4.0m,d3=10| 3 |
(1)粒子离开区域Ⅰ时的速度大小;
(2)粒子从区域Ⅱ进入区域Ⅲ时的速度方向与边界面的夹角;
(3)粒子从O点开始到离开Ⅲ区域时所用的时间.
分析:(1)由动能定理列方程求粒子离开区域Ⅰ时的速度大小;
(2)粒子在区域Ⅱ中竖直方向匀速直线运动,水平方向匀加速直线运动,即粒子做类平抛运动,由类平抛运动规律求解;
(3)先求出粒子在Ⅲ区域的运动半径,然后做出轨迹,确定圆周运动转过的圆心角,结合周期公式T=
求解Ⅲ区域的运动时间,总时间为三段运动的时间之和.
(2)粒子在区域Ⅱ中竖直方向匀速直线运动,水平方向匀加速直线运动,即粒子做类平抛运动,由类平抛运动规律求解;
(3)先求出粒子在Ⅲ区域的运动半径,然后做出轨迹,确定圆周运动转过的圆心角,结合周期公式T=
| 2πm |
| qB |
解答:解:(1)对粒子在区域Ⅰ运动过程,由动能定理得:
mv12=qEId1…①
得:v1=4×103m/s…②
(2)粒子在区域Ⅱ做类平抛运动.水平向右为y轴,竖直向上为x轴.设粒子进入区域Ⅲ时速度与边界的夹角为θ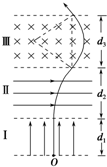
tan θ=
…③
vx=v1 vy=at…④
a=
…⑤
t=
…⑥
把数值代入得:θ=30°⑦
(3)粒子进入磁场时的速度为:v2=2v1…⑧
粒子在磁场中运动的半径为:R=
=10m…⑨
粒子在磁场中运动所对的圆心角为120°,因此有:
t3=
×
qE1=ma1v1=a1t1
由(2)得:t2=10-3st=t1+t2+t3=(3.5+
)×10-3s=6.12×10-3s
答:(1)粒子离开区域Ⅰ时的速度大小4×103m/s;
(2)粒子从区域Ⅱ进入区域Ⅲ时的速度方向与边界面的夹角θ=30°;
(3)粒子从O点开始到离开Ⅲ区域时所用的时间6.12×10-3s.
| 1 |
| 2 |
得:v1=4×103m/s…②
(2)粒子在区域Ⅱ做类平抛运动.水平向右为y轴,竖直向上为x轴.设粒子进入区域Ⅲ时速度与边界的夹角为θ

tan θ=
| vx |
| vy |
vx=v1 vy=at…④
a=
| qE2 |
| m |
t=
| d2 |
| v1 |
把数值代入得:θ=30°⑦
(3)粒子进入磁场时的速度为:v2=2v1…⑧
粒子在磁场中运动的半径为:R=
| mv2 |
| qB |
粒子在磁场中运动所对的圆心角为120°,因此有:
t3=
| 1 |
| 3 |
| 2πm |
| qB |
qE1=ma1v1=a1t1
由(2)得:t2=10-3st=t1+t2+t3=(3.5+
| 5π |
| 6 |
答:(1)粒子离开区域Ⅰ时的速度大小4×103m/s;
(2)粒子从区域Ⅱ进入区域Ⅲ时的速度方向与边界面的夹角θ=30°;
(3)粒子从O点开始到离开Ⅲ区域时所用的时间6.12×10-3s.
点评:粒子在电场中的偏转情况,一定注意化曲为直,即将运动分解为平行于电场的方向与垂直于电场的方向;粒子在磁场中的运动一定要注意找出圆心和半径,进而能正确的应用好几何关系,则可顺利求解!

练习册系列答案
相关题目
 (2013?厦门一模)如图所示,光滑轨道ABCD固定在竖直平面内,由直轨道AB与圆弧轨道BCD平滑相切对接组成.圆弧的圆心为O点,半径大小为R,OB与竖直方向OC夹角θ=37°,D点与圆心O点等高;竖直且过B点的直线PQ右侧空间内,被水平且过O点、D点的直线MN分为下区域Ⅰ和上区域Ⅱ,下区域Ⅰ内存在水平向右的匀强电场,场强为
(2013?厦门一模)如图所示,光滑轨道ABCD固定在竖直平面内,由直轨道AB与圆弧轨道BCD平滑相切对接组成.圆弧的圆心为O点,半径大小为R,OB与竖直方向OC夹角θ=37°,D点与圆心O点等高;竖直且过B点的直线PQ右侧空间内,被水平且过O点、D点的直线MN分为下区域Ⅰ和上区域Ⅱ,下区域Ⅰ内存在水平向右的匀强电场,场强为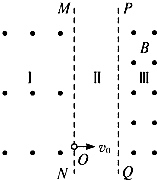 如图所示,相互平行的竖直分界面MN、PQ,相距L,将空间分为Ⅰ、Ⅱ、Ⅲ区.Ⅰ、Ⅲ区有水平方向的匀强磁场,Ⅰ区的磁感应强度未知,Ⅲ区的磁感应强度为B;Ⅱ区有竖直方向的匀强电场(图中未画出).一个质量为m、电荷量为e的电子,自MN上的O点以初速度v0水平射入Ⅱ区,此时Ⅱ区的电场方向竖直向下,以后每当电子刚从Ⅲ区进入Ⅱ区或从Ⅰ区进入Ⅱ区时,电场突然反向,场强大小不变,这个电子总是经过O点且水平进入Ⅱ区.(不计电子重力)
如图所示,相互平行的竖直分界面MN、PQ,相距L,将空间分为Ⅰ、Ⅱ、Ⅲ区.Ⅰ、Ⅲ区有水平方向的匀强磁场,Ⅰ区的磁感应强度未知,Ⅲ区的磁感应强度为B;Ⅱ区有竖直方向的匀强电场(图中未画出).一个质量为m、电荷量为e的电子,自MN上的O点以初速度v0水平射入Ⅱ区,此时Ⅱ区的电场方向竖直向下,以后每当电子刚从Ⅲ区进入Ⅱ区或从Ⅰ区进入Ⅱ区时,电场突然反向,场强大小不变,这个电子总是经过O点且水平进入Ⅱ区.(不计电子重力)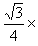 105 V/m,方向水平向右,Ⅲ区域磁感应强度B=5.0 T,方向垂直纸面向里,三个区域宽度分别为d1=5.0 m,d2=4.0 m,d3=10 m。一质量m=1.0×10-8 kg、电荷量q=1.6×10-6 C的粒子从O点由静止释放,粒子重力忽略不计。求:
105 V/m,方向水平向右,Ⅲ区域磁感应强度B=5.0 T,方向垂直纸面向里,三个区域宽度分别为d1=5.0 m,d2=4.0 m,d3=10 m。一质量m=1.0×10-8 kg、电荷量q=1.6×10-6 C的粒子从O点由静止释放,粒子重力忽略不计。求: