题目内容
16.设行星A和行星B都是均匀球体,A与B的质量之比mA:mB=2:1,A与B的半径之比RA:RB=1:2,行星A的卫星a沿圆轨道运行的周期为Ta,行星B的卫星b沿圆轨道运行的周期为Tb,两卫星的轨道都非常接近各自的行星表面,则它们运行的周期之比为1:4.分析 卫星做圆周运动,万有引力提供向心力,求出周期和中心天体质量M以及运行半径R之间的关系可得.
解答 解:卫星做圆周运动时,万有引力提供圆周运动的向心力,则有:
G$\frac{Mm}{{R}^{2}}$=mR$\frac{4{π}^{2}}{{T}^{2}}$
解得:
T=2π $\sqrt{\frac{{R}^{3}}{GM}}$
两卫星运行周期之比为:
$\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{(\frac{{R}_{1}}{{R}_{2}})^{3}\frac{{M}_{2}}{{M}_{1}}}$=$\sqrt{\frac{1}{8}×\frac{1}{2}}$=$\frac{1}{4}$
故答案为:1:4
点评 根据万有引力提供向心力列出方程,得到周期之比和半径以及质量之间的关系,代入数据可得结论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.在研究物体的运动时,下列可以当作质点处理的是( )
| A. | 研究某学生骑自行车回校的速度 | |
| B. | 对这位学生骑车姿势进行生理学分析 | |
| C. | 研究火星探测器从地球到火星的飞行轨迹 | |
| D. | 研究火星探测器降落火星后如何探测火星的表面 |
7.有三个阻值都是12欧姆的电阻,将它们用各种方法连接后,不可能得到的等效电阻值为( )
| A. | 4欧 | B. | 12欧 | C. | 18欧 | D. | 36欧 |
4.以下说法中正确的是( )


| A. | 在如图所示的双缝干涉现象中,当两缝间的距离及挡板和屏的距离一定时.红光的相邻条纹间距比蓝光相邻条纹间距小 | |
| B. | 真空中的光速在不同的惯性参考系中都是相同的与光源、观察者间的相对运动没有关系 | |
| C. | 市场上烤制鸡鸭等肉类食品的“远红外烤箱”,其热作用主要是靠红外线来实现的 | |
| D. | 著名的泊松亮斑是光的衍射现象 | |
| E. | 两列频率相同的水面波能产生干涉,形成的稳定的干涉图样,连线的中垂线必为加强区 | |
| F. | 光导纤维有很多的用途,它由内芯和外套两层组成,外套的折射率比内芯要大 |
11.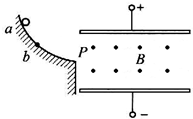 如图所示,带电平行板中存在有垂直纸面向外匀强磁场,某带电小球沿光滑绝缘轨道上的a点由静止开始下滑,经过轨道末端P点后进入平行板间恰好能沿水平方向作直线运动.现使小球从较低的b点开始下滑,经P点进入板间,则带电小球在平行板间的运动过程中下列说法正确的是( )
如图所示,带电平行板中存在有垂直纸面向外匀强磁场,某带电小球沿光滑绝缘轨道上的a点由静止开始下滑,经过轨道末端P点后进入平行板间恰好能沿水平方向作直线运动.现使小球从较低的b点开始下滑,经P点进入板间,则带电小球在平行板间的运动过程中下列说法正确的是( )
 如图所示,带电平行板中存在有垂直纸面向外匀强磁场,某带电小球沿光滑绝缘轨道上的a点由静止开始下滑,经过轨道末端P点后进入平行板间恰好能沿水平方向作直线运动.现使小球从较低的b点开始下滑,经P点进入板间,则带电小球在平行板间的运动过程中下列说法正确的是( )
如图所示,带电平行板中存在有垂直纸面向外匀强磁场,某带电小球沿光滑绝缘轨道上的a点由静止开始下滑,经过轨道末端P点后进入平行板间恰好能沿水平方向作直线运动.现使小球从较低的b点开始下滑,经P点进入板间,则带电小球在平行板间的运动过程中下列说法正确的是( )| A. | 小球带正电 | |
| B. | 小球将能再次沿水平方向作直线运动 | |
| C. | 小球所受的洛伦兹力将会减小 | |
| D. | 小球的电势能和动能都增大 |
8.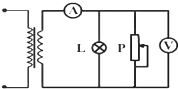 如图为一理想变压器,现在原线圈两端加上正弦式交变电压U=30$\sqrt{2}$sin(100πt)V,灯泡L的额定电压为6V且正常发光,电压表和电流表可视为理想电表.则下列说法中正确的是( )
如图为一理想变压器,现在原线圈两端加上正弦式交变电压U=30$\sqrt{2}$sin(100πt)V,灯泡L的额定电压为6V且正常发光,电压表和电流表可视为理想电表.则下列说法中正确的是( )
 如图为一理想变压器,现在原线圈两端加上正弦式交变电压U=30$\sqrt{2}$sin(100πt)V,灯泡L的额定电压为6V且正常发光,电压表和电流表可视为理想电表.则下列说法中正确的是( )
如图为一理想变压器,现在原线圈两端加上正弦式交变电压U=30$\sqrt{2}$sin(100πt)V,灯泡L的额定电压为6V且正常发光,电压表和电流表可视为理想电表.则下列说法中正确的是( )| A. | 原、副线圈的匝数之比为5$\sqrt{2}$:1 | |
| B. | 该交流电的频率为100Hz | |
| C. | 若将变阻器的滑片P向上滑动,电流表读数变大,电压表读数不变 | |
| D. | 若将变阻器的滑片P向上滑动,变压器的输出功率变小 |
5.如图所示,质量为m的物体,在力F的作用下,静止于竖直墙面上,则下列说法正确的是( )


| A. | 物体受到竖直向上的静摩擦力的作用 | |
| B. | 物体受到竖直向上的滑动摩擦力的作用 | |
| C. | 物体所受摩擦力随F的增大而增大 | |
| D. | 物体所受摩擦力大小为mg |