题目内容
1.一杂技运动员骑摩托车沿一竖直圆轨道做匀速圆周运动,若车速恒为20m/s,人与车的质量之和为200㎏,轮胎与轨道间的动摩擦因数为0.1,车通过最低点A时,发动机的功率为20kw,求车通过最高点时发动机的功率.分析 在最低点时对人和车受力分析:重力与支持力的合力作为向心力,由向心力的公式可以求得车受到的支持力,再由P=Fv和f=FN即可求得圆轨道的半径;
由向心力的公式可以求得车通过最高点B时对轨道的压力,再由瞬时功率的公式可以求得通过最高点B时发动机的功率.
解答 解:在A点,设发动机功率为PA,则 PA=μFAV,
解得车受到的支持力为 FA=10000N,
车通过最低点A时对轨道的压力:FA-mg=$m\frac{{v}^{2}}{R}$.
在B点人与车整体所需向心力大小与在A点的向心力相等,即:
$m\frac{{v}^{2}}{R}$=FA-mg=10000N-2000N=8000N
在B点,FB+mg=$m\frac{{v}^{2}}{R}$,
解得车通过最高点B时对轨道的压力:
FB=$m\frac{{v}^{2}}{R}$-mg=6000N,
则车通过最高点A时发动机的功率 PB=μFBv=12000W=12KW.
答:车通过最高点B时发动机的功率是12KW.
点评 发动机的功率时要注意用瞬时功率的公式,车在最高点和最低点时对车受力分析,应用圆周运动的公式即可求得对轨道的压力和发动机的功率

练习册系列答案
相关题目
12.关于甲、乙、丙、丁四个物体的运动下面说法正确的是( )


| A. | 甲图若是位移-时间图象,则甲物体可能是匀变速直线运动的 | |
| B. | 乙图若是加速度-时间图象,则乙物体可能是匀变速直线运动的 | |
| C. | 丙图若是速度-时间图象,则丙物体可能是自由落体运动的 | |
| D. | 丁位移-时间图象,则丁物体可能是匀加速直线运动的 |
9.为了测量某电池的电动势E(约为3V)和内阻r,可供选择的器材如下:
A.电流表G1(2mA内电阻为l00Ω) B.电流表G2(1mA内阻未知)
C.电阻箱R1(0~99.9Ω) D.电阻箱R2(0~9999.9Ω)
E.滑动变阻器R3(0~l0Ω1A) F.滑动变阻器R4(0-1000Ω10mA)
G.定值电阻R0(800Ω 0.1A) H.待测电池
I.导线、电键若干
(1)采用如图(甲)所示的电路,测定电流表G2的内阻,得到电流表G1的示数I1、电流表G2的示数I2如表所示:
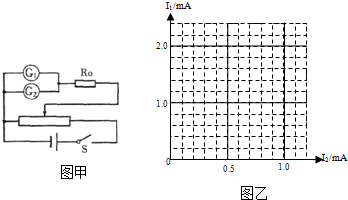
根据测量数据,请在图(乙)坐标中描点作出I1-I2图线,由图线可得出电流表G2的内阻等于2.0×102Ω.
(2)某同学在现有器材的条件下,要测量该电池的电动势和内阻,采用了图(丙)的电路,若把电流表G2改装成量程为3V的电压表,则电阻箱①该调到2.8×103Ω.把电流表G1改装成量程为0.5A的电流表,则电阻箱②该调到0.40Ω,(该结果保留二位有效数字).
(3)以G2示数I2为纵坐标,G1示数I1为横坐标,作出l1-l2图象如图(丁)所示,结合图象可得出电源的电动势为2.7V,电源的内阻为8.6Ω(结果均保留二位有效数字

A.电流表G1(2mA内电阻为l00Ω) B.电流表G2(1mA内阻未知)
C.电阻箱R1(0~99.9Ω) D.电阻箱R2(0~9999.9Ω)
E.滑动变阻器R3(0~l0Ω1A) F.滑动变阻器R4(0-1000Ω10mA)
G.定值电阻R0(800Ω 0.1A) H.待测电池
I.导线、电键若干
(1)采用如图(甲)所示的电路,测定电流表G2的内阻,得到电流表G1的示数I1、电流表G2的示数I2如表所示:
| I1(mA) | 0.40 | 0.81 | 1.20 | 1.59 | 2.00 |
| I2(mA) | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 |

根据测量数据,请在图(乙)坐标中描点作出I1-I2图线,由图线可得出电流表G2的内阻等于2.0×102Ω.
(2)某同学在现有器材的条件下,要测量该电池的电动势和内阻,采用了图(丙)的电路,若把电流表G2改装成量程为3V的电压表,则电阻箱①该调到2.8×103Ω.把电流表G1改装成量程为0.5A的电流表,则电阻箱②该调到0.40Ω,(该结果保留二位有效数字).
(3)以G2示数I2为纵坐标,G1示数I1为横坐标,作出l1-l2图象如图(丁)所示,结合图象可得出电源的电动势为2.7V,电源的内阻为8.6Ω(结果均保留二位有效数字

6.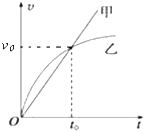 甲、乙两汽车在一平直公路上同向行驶,它们的速度-时间图象如图所示,则下列说法正确的是( )
甲、乙两汽车在一平直公路上同向行驶,它们的速度-时间图象如图所示,则下列说法正确的是( )
 甲、乙两汽车在一平直公路上同向行驶,它们的速度-时间图象如图所示,则下列说法正确的是( )
甲、乙两汽车在一平直公路上同向行驶,它们的速度-时间图象如图所示,则下列说法正确的是( )| A. | t0时刻甲车运动的加速度等于乙车运动的加速度 | |
| B. | t0时刻甲、乙两车相遇 | |
| C. | 0~t0时间内,甲车的平均速度大于乙车的平均速度 | |
| D. | 汽车乙的平均速度大于$\frac{v_0}{2}$ |
13.水平放置的平行板电容器两板间距离为d,极板保持跟电源相连,电容器上板中心有一小孔(小孔对电场的影响可以忽略不计),小孔的正上方d处的P点有一带电粒子,该粒子从静止开始下落,经过小孔进入电容器,并在下极板处(未与极板接触)返回.之后将下极板向上平移$\frac{d}{3}$,再从P点静止释放相同的粒子,下列说法正确的是( )
| A. | 粒子下落到最低点的过程中,减少的重力势能大于增加的电势能 | |
| B. | 粒子下落到最低点的过程中,减少的机械能等于增加的电势能 | |
| C. | 第二次释放粒子,粒子将在距上板$\frac{d}{2}$处返回 | |
| D. | 第二次释放粒子,粒子将在距上板$\frac{d}{3}$处返回 |
11.关于磁感应强度说法正确的是( )
| A. | 由B=$\frac{F}{IL}$可知,B与F成正比,与IL成反比 | |
| B. | 垂直于磁场放置的通电导线的受力方向就是磁感应强度的方向 | |
| C. | 磁感应强度方向与磁感线指向垂直 | |
| D. | 在任何情况下B的方向与小磁针N极受力方向一致 |
 如图所示,设匀强磁场的磁感应强度B为0.10T,矩形线框向左匀速运动的速度v为5.0m/s,长度l为40cm的一条边在磁场中切割磁感线,整个线框的电阻R为0.50Ω.试求:
如图所示,设匀强磁场的磁感应强度B为0.10T,矩形线框向左匀速运动的速度v为5.0m/s,长度l为40cm的一条边在磁场中切割磁感线,整个线框的电阻R为0.50Ω.试求: