Question

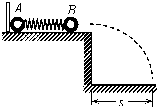质量相等的A、B两球之间压缩一根轻弹簧，静置于光滑台面上．当用板挡住小球A而只释放B球时，B球被弹出落于桌边距离为s的水平地面上，如图所示．问当用同样的程度压缩弹簧，取走A左边的挡板，将A、B同时释放，B球的落地点离桌边为（　　）

• A、

  s

  2

• B、

  2

  s
• C、s
• D、

  2

  2

  s

Answer 1

分析：A、B两球之间压缩一根轻弹簧，当用板挡住A球而只释放B球时，弹性势能完全转化为B球的动能，以一定的初速度抛出，借助于抛出水平位移可确定弹簧的弹性势能．当用同样的程度压缩弹簧，取走A左边的挡板，将A、B同时释放，由动量守恒定律与机械能守恒定律可求出B球获得的速度，再由平抛运动规律可算出抛出的水平位移．

解答：解：当用板挡住A球而只释放B球时，B球做平抛运动．设高度为h，则有vB=s

g 2h

，所以弹性势能为
E=

1

2

m

v

2 B

=

mgs2

4h

，当用同样的程度压缩弹簧，取走A左边的挡板，将A、B同时释放，由动量守恒定律可得：
0=mv_A-mv_B 所以v_A：v_B=1：1．因此A球与B球获得的动能之比E_kA：E_kB=1：1．所以B球的获得动能为：

mgs2

8h

．
那么B球抛出初速度为v_B=

s

2

g h

，
则平抛后落地水平位移：x=

s

2

g h

×

2h g

=

2

2

s，
故选：D

点评：考查动量守恒定律、机械能守恒定律，及平抛运动规律．两种情况下，弹性势能完全相同．在弹簧恢复过程中弹性势能转化为动能．