题目内容
如图所示，ABCD为固定的水平光滑矩形金属导轨，AB间距离为L，左右两端均接有阻值为R的电阻，处在方向竖直向下、磁感应强度大小为B的匀强磁场中，质量为m、长为L的导体棒MN放在导轨上，甲、乙两根相同的轻质弹簧一端均与MN棒中点固定连接，另一端均被固定，MN棒始终与导轨垂直并保持良好接触，导轨与MN棒的电阻均忽略不计.初始时刻，两弹簧恰好处于自然长度，MN棒具有水平向左的初速度v0，经过一段时间，MN棒第一次运动至最右端，这一过程中AB间电阻R上产生的焦耳热为Q，则（ ）
A.初始时刻棒受到安培力大小为
B.从初始时刻至棒第一次到达最左端的过程中，整个回路产生焦耳热小于
C.当棒再次回到初始位置时，AB间电阻R的功率小于
D.当棒第一次到达最右端时，甲弹簧具有的弹性势能为mv20-Q
ACD
【解析】
试题分析：初始时刻棒受到的力的作用，应该考虑到初始时刻弹簧没有形变，此时棒受力应为安培力，棒产生的感应电动势为E=BLv0，整个回路由棒以及两个并联的阻值为R的电阻组成，所以电流为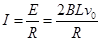
，则安培力为
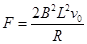，所以A正确；B项不能定量计算，但是可以通过定性分析得出将棒向左开始运动运动到最右端分为3个过程，过程一，从初始位置到最左端，过程二，从最左端回到初始位置，过程三，从初始位置到最右端，在整个过程中，不断有动能转化成焦耳热，所以动能不断减小，速度也就不断减小，所以第一个过程产生的焦耳热应该大于整个过程产生的焦耳热的
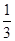，而整个过程中AB间电阻和CD间电阻产生焦耳热一样多，总量为2Q，所以，第一个过程产生的焦耳热Q1＞
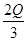，故B错误；C中由于动能减少，再回到初始位置时的速度应小于开始运动的初速度，所以此时AB间电阻的功率P＜P0，
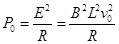，所以C正确；D项用能量的观点来说明，当棒到达最右端时，所有的动能都转化成了焦耳热和弹簧的弹性势能，整个回路产生的焦耳热为2Q，又由两根弹簧形变量相同，能量在转化过程中总量守恒，所以甲弹簧的弹性势能为Ep=mv20-Q，故D正确，所以该题答案为ACD。
考点：本题考查了电磁感应中的能量转化
名校课堂系列答案
如图所示，ABCD为一倾角θ=30°的粗糙斜面，AD边与BC边平行，有一重力G=10N放在斜面上，当对物体施加一个与AB边平行的拉力F时，物体恰能做匀速直线运动．已知物体与斜面的动摩擦因数μ=
如图所示，abcd为质量M=2㎏的导轨，放在光滑绝缘的水平面上，另有一根质量m=0.6㎏的金属棒PQ平行bc放在水平导轨上，PQ棒左边靠着绝缘的竖直立柱e、f，导轨处于匀强磁场中，场以00′为界，左侧的磁场方向竖直向上，右侧的磁场方向水平向右，磁感强度都为B=0.8T．导轨的bc段长L=0.5m，其电阻r=0.4Ω，金属棒的电阻R=0.2Ω，其余电阻均可不计，金属棒与导轨间的动摩擦因数为0.2．若导轨上作用一个方向向左、大小为F=2N的水平拉力，设导轨足够长，g取10m/s2．试求：
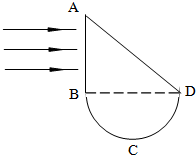如图所示，ABCD为同种材料构成的柱形透明体的横截面，其中ABD部分为等腰直角三角形，BCD部分为半圆形，一束单色平行光从真空射向AB或AD面，材料折射率n=1.6，下列说法正确的是（ ）| A、从AB面中点射入的光线一定从圆弧的中点射出 | B、从AB面射入的所有光线经一次反射和折射后都从BCD面射出 | C、从AB面中间附近射入的所有光线经一次反射和折射后都从BCD面射出 | D、若光线只从AD面垂直射入，则一定没有光线从BCD面射出 |
如图所示，ABCD为一直角梯形棱镜的截面，∠C=60°P为垂直于直线BC的光屏，现用一宽度等于AB边的单色平行光束垂直射向AB面，经棱镜折射后在屏P上形成宽度等于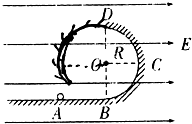
如图所示，ABCD为竖直放在场强为E=104V/m水平匀强电场中的绝缘光滑轨道，其中轨道的BCD部分是半径为R的圆形轨道，轨道的水平部分与其半圆相切，A为水平轨道上的一点，而且AB=R=0.2m，把一质量m=0.1kg、带电荷量q=+1×10-4C的小球放在水平轨道的A点由静止开始释放，小球在轨道的内侧运动．（g取10m/s2）求：